variação da resistência com a temperatura 

Podemos observar dois fenômenos simultâneos, quando percebemos que a temperatura de um fio de material condutor aumenta. Estes fenômenos se contrapõem entre si. 

Vejamos quais são esses fenômenos: 
1- Com a temperatura alta, algumas partículas que fazem parte do meio condutor começam a vibrar com mais intensidade, e com isso a possibilidade de ocorrer choques entre as partículas que estão na corrente elétrica são maiores, ou seja, é por isso que acontece o aumento da resistência elétrica. 

2- Com a temperatura alta, um número grande de elétrons livres que compõe um material condutor, deixa seus átomos e passam a fazer parte de uma nuvem eletrônica, porém se a densidade dos elétrons aumentar, a corrente passa a ser mais intensa, e a resistência elétrica diminui. 

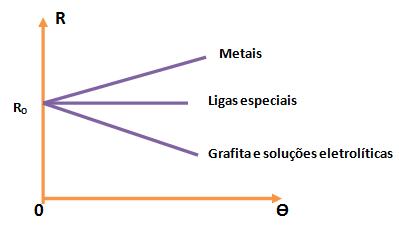
Em metais predominam o efeito 1, aumentando assim a sua resistência elétrica com a temperatura, porém em algumas ligas metálicas, como por exemplo, a manganima e a niquelina, os dois efeitos se compensam entre si e suas resistências continuam constantes com a temperatura. 

Já o efeito 2 predomina na grafita, e sua resistência é decrescente com o aumento da temperatura. 

Em algumas soluções como, por exemplo, as de eletrólitos, a resistência também é decrescente com o aumento da temperatura, mas por outra razão: a temperatura alta faz com que as dissociações iônicas aumentem o seu grau, ou seja, aumentem seu número de íons que compõem a corrente elétrica. Essa resistência decrescente faz também com que a viscosidade do solvente diminua, fazendo com que os íons que compõem a corrente, se movimente mais facilmente. 

Vejamos agora um gráfico que representa a teoria acima: 

Para descobrirmos o valor aproximado da resistência R em uma determinada temperatura ø, devemos usar a função abaixo: 

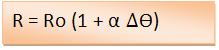
Onde nesta função Ro representa a resistência elétrica na temperatura inicial ø0, e α é o coeficiente de temperatura do material. 

Devemos lembrar que o coeficiente de temperatura α é totalmente dependente do material e do valor da temperatura. Porém, como você deve ter percebido no gráfico, permitimos α constante independente da temperatura, mas sendo isso apenas uma hipótese aproximada. 

Com base no gráfico acima, temos: 

Para os metais: α > 0
Para as ligas especiais α = 0
Para a grafita e as soluções eletrolíticas α < 0. Quando comparada com a variação de resistência com a temperatura, a dilatação térmica é desprezível. Considerando 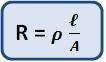 podemos concluir que a variação de resistência com a temperatura ocorre devido à variação da resistividade com a temperatura.