Movimentos particulares de uma partícula eletrizada num campo magnético uniforme 

Para entendermos melhor a respeito desse movimento, vamos pensar em um campo magnético uniforme, onde uma partícula eletrizada foi atirada. Essa situação nos permite estudar três casos, onde em cada caso a partícula se comportará de maneira diferente.

Vejamos: 

1° caso: lançamento paralelo ao campo 
Neste caso a partícula irá ser atirada paralelamente às linhas de indução do campo magnético. 

Caso se a partícula for atirada com o mesmo sentido do campo, teremos: 

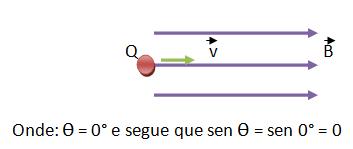
Já se a partícula for atirada no sentido contrário do campo, teremos: 

Pelo fato de existir a inércia, a partícula irá continuar a se movimentar em movimento retilíneo e uniforme no campo magnético. Portanto concluímos que a carga elétrica que é atirada na direção das linhas de indução do campo executa um movimento retilíneo e uniforme.

2° caso: lançamento perpendicular ao campo 

Vejamos a ilustração abaixo que nos mostra a partícula eletrizada sendo atirada perpendicularmente às linhas de indução de um ponto do campo magnético. 

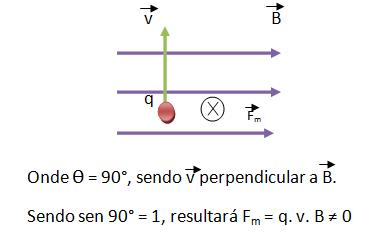
Quando se obtêm um resultado para o módulo da força magnética, significa que esse módulo é constante, pelo fato da carga (q), do módulo da velocidade (v), e da intensidade B do campo, não variar. Com isso a partícula que fica sob a ação de uma força com intensidade constante, possuirá uma direção perpendicular à velocidade. Portanto podemos concluir que quando uma partícula eletrizada é atirada em uma direção perpendicular às linhas de indução de qualquer campo magnético uniforme, ela irá realizar um movimento circular e uniforme. 

Essa partícula irá realizar uma trajetória circular situada em um plano perpendicular às linhas de indução do campo. 

Vejamos a ilustração: 

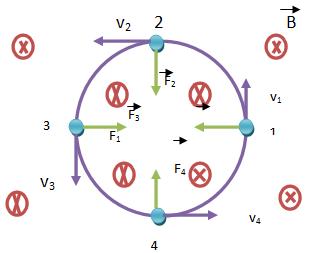
Cálculo do raio da trajetória 
Para que possamos entender melhor sobre este cálculo, vamos pensar em uma partícula atirada perpendicularmente ao campo magnético, fazendo com que sua trajetória seja em forma de circunferência. Como já sabemos a força magnética Fm é considerada uma força centrípeta Fcp. Portanto podemos fazer uma comparação entre as duas fórmulas, para que possamos calcular o raio R. 

Vejamos: 

Cálculo do período 
Considerando que uma partícula foi atirada em uma direção perpendicular às linhas de indução de um campo magnético (B), realizando assim um movimento circular e uniforme. O período T significa o intervalo de tempo gasto numa volta. Vejamos então como determinar esse intervalo de tempo: 

Pensando em uma volta temos: 

Vejamos a seguir duas observações: 

2– É importante sabermos também que tanto a freqüência como o período, não são dependentes da velocidade de lançamento.

3° caso: a partícula é lançada obliquamente no campo B 
Neste caso, vamos atirar a partícula eletrizada, obliquamente às linhas de indução de um campo magnético e uniforme, fazendo com que o ângulo formado pelo lançamento não seja nem de 180°, nem de 90° e nem de 0°.
 
Vejamos a ilustração abaixo: 


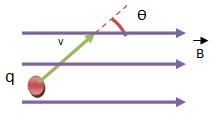
Com base na figura acima, podemos observar que a força magnética(Fm), possui uma intensidade representada por:


Considerando um vetor velocidade v, “dentro” de duas componentes perpendiculares, representadas por v1 e v2, como podemos ver na figura acima, sendo que uma das direções é considerada paralela às linhas de indução e a outra é perpendicular às linhas. 

Vejamos: