Cinemática do M.H.S.
Por Redação
Cinemática do M. H. S
Visualização do M. H. S
Observando a figura abaixo, iremos ver uma roda circular com uma manivela M, onde a roda que é posta em um plano vertical é iluminada pela luz do “sol a pino”, que aparece no solo, suposto plano e horizontal, as sombra M’ de M.
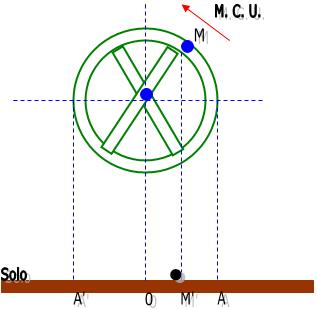
A roda é colocada em movimento de rotação uniforme, girando no sentido anti-horário, onde M passa a ter um M.C. U com uma velocidade angular dada por:
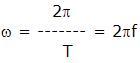
Onde:
T é o período do movimento;
F é a freqüência do movimento.
Conforme M for se movimentando, sua sombra M’ irá se movimentar correspondentemente. Quando percorre no sentido anti-horário a semicircunferência superior, M faz M’ se deslocar retilineamente de A para A’. Pode ocorrer também que ao percorrer também no sentido anti-horário a semicircunferência inferior, M faz M’ se deslocar retilineamente agora de A para A’.
Portanto podemos concluir que ao ocorrer o M.C.U, irá fazer sua sombra M’ descrever no solo, o movimento retilíneo, oscilatório, com período T e freqüência f, sendo assim limitados pelos pontos A e A’, que são eqüidistantes do ponto O. É importante ressaltarmos que A e A’ são pontos de inversão do movimento oscilatório de M’.
Recebe o nome de Movimento Harmônico Simples (M.H.S) o movimento retilíneo e oscilatório de M’, que é tido através da projeção diametral do M.C.H. de M.
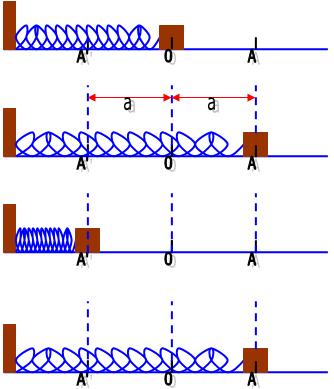
O oscilador massa – mola horizontal
A figura a seguir mostra um bloco que está em repouso, colocado em um plano liso e horizontal. O bloco que está acoplado em uma mola elástica, com isso o bloco vai para o ponto A, deixando o local que está. Esse bloco ganha um movimento para a esquerda, tendo assim uma velocidade nula no ponto A’.
Vejamos:
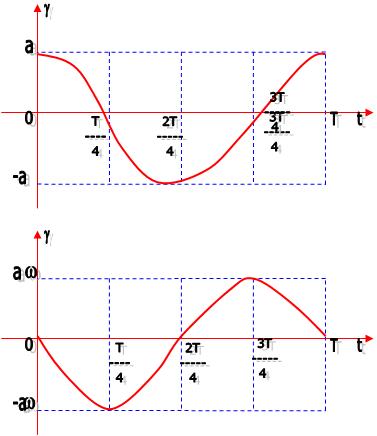
Função horária no M. H. S: x = f(t).
O Movimento Harmônico Simples (M. H. S) é considerado todo movimento retilíneo e oscilatório, onde a abscissa x (denominada elongação) altera com o tempo t, conforme a função do tipo:

Vejamos um exemplo, que nos mostra um movimento harmônico simples:
Em alguns relógios do tipo cuco, o boneco oscila verticalmente preso a uma mola. O período das oscilações é igual a um segundo e o movimento do boneco é harmônico e simples, como mostra a figura abaixo:

Com o objetivo de deduzir a função x = f(t) para o M.H. S devemos considerar a seguinte situação:
Uma partícula P realiza M.C. U no sentido anti-horário na circunferência de raio a representada.
Na figura que veremos a seguir, o ângulo horário é considerado o ângulo que é formado pelo raio que girante OP e o eixo de referência.
É importante lembrarmos que P faz o M.C.U, onde o ângulo horário é dado em função do tempo t através da expressão:
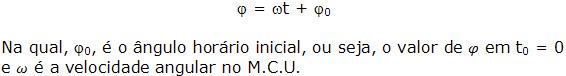
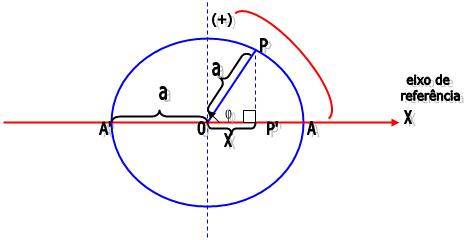
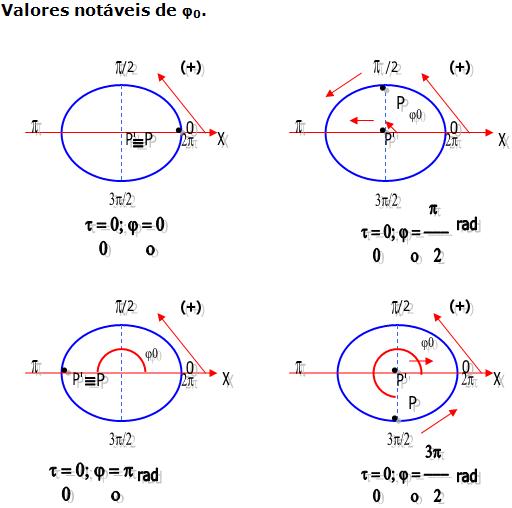
De acordo com a figura acima, podemos perceber que enquanto P faz o seu M.C.U, sua projeção P´ vai descrevendo sobre o seu diâmetro AA’, um M.H.S., sendo assim limitado pelos pontos A e A’. Para que se tenha a função x = f(t), devemos orientar a trajetória de P’ para a direita, fixando assim a sua origem em O, que é o centro da circunferência e ponto de equilíbrio do M.H.S. Portanto podemos concluir que no triângulo retângulo OPP’, tem-se:

Função de velocidade escalar no M. H. S.: V = f(t)
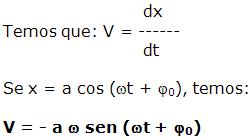
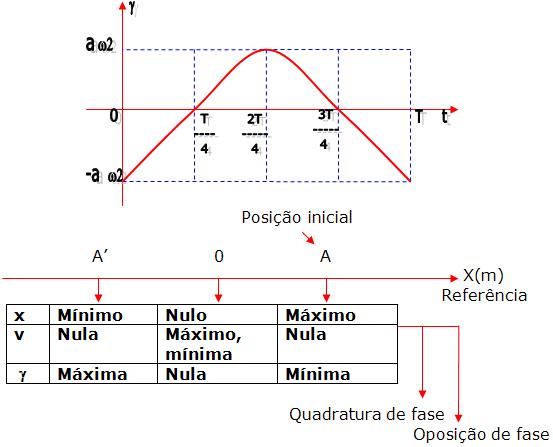
Função de aceleração escalar no M. H. S.:
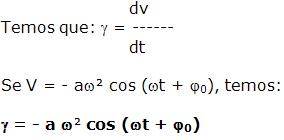
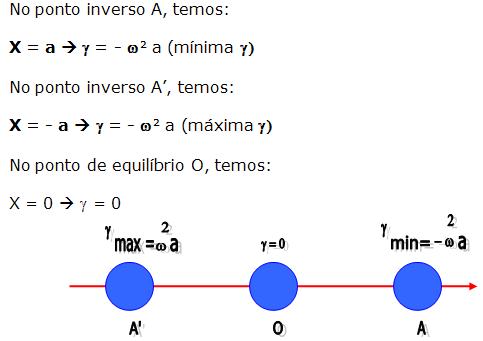
Relação entre a aceleração escalar e a elongação no M. H. S.

A aceleração escalar no M.H.S é proporcional à elongação com o sinal invertido, onde o coeficiente de proporcionalidade é o quadrado da pulsação.
Diagramas horários no M. H. S. Considerando um M. H. S., na qual sua elongação se diversifica com o decorrer do tempo, temos a seguinte função: