Composição de velocidade 
                                                →   →    →
Considerando a expressão r = r1 + r2, temos: 

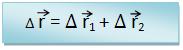
Nota: 

* No caso acima, podemos considerar o vetor deslocamento do ponto P (no movimento resultante), a soma dos vetores deslocamento no movimento relativo e também no movimento de arrastamento. 

Vejamos: 

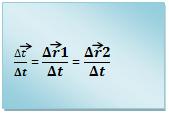
É importante lembrar que a razão entre o vetor de deslocamento e o intervalo de tempo é considerada a velocidade vetorial média, com isso temos: 

Porém quando Δt equivale à zero, temos: 

Nota:

*Não podemos esquecer que a velocidade no movimento resultante, consiste na soma das velocidades nos movimentos relativos e também nos movimentos de arrastamento. Vejamos: 

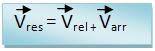
Com base nas funções acima, podemos traduzir o teorema de Roberval, vejamos o exemplo: 

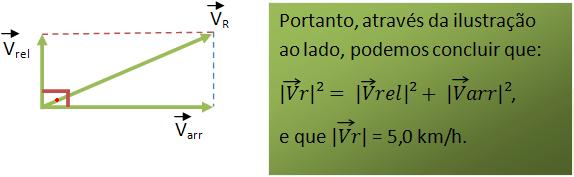
Vamos pensar no vagão de um trem que atinge uma velocidade constante de intensidade de aproximadamente 4,0 km/h, em relação ao seu trajeto. 

Uma pessoa que está andando em cima do vagão com uma velocidade constante de intensidade, de aproximadamente 3,0 km/h, com relação ao vagão. Sendo que esta pessoa está na direção perpendicular à velocidade do vagão. 

Para cada movimento, a pessoa apresenta uma velocidade diferente. Vejamos: 

* No movimento relativo, a velocidade da pessoa em relação ao vagão é |Vrel|=3,0 km/h. 

* No movimento de arrastamento, a velocidade da pessoa em relação ao vagão é |Varr|= 4,0 km/h. 

* No movimento resultante, a velocidade da pessoa em relação ao movimento é de 5,0 km/h, 

Vejamos: