Aplicação
Num bar do Coroado, o Adelino, físico e exímio jogador de bilhar, aplica uma tacada na bola comunicando-lhe uma velocidade de módulo 4,0m/s. Sabendo-se que, inicialmente, a bola estava em repouso e que a tacada teve duração de 1,0.10-2s, calcular a intensidade média da força aplicada pelo taco à bola.
Solução:
Admitindo que a força aplicada pelo taco seja a resultante paralela ao movimento, apliquemos o Teorema do Impulso:
Itotal = Qfinal – Qinicial
Como a bola estava inicialmente em repouso, tem-se Qinicial = 0:
Itotal = Qfinal = mvfinal (I)
No caso, Itotal pode ser calculado por:
Itotal = Fm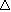
Comparando (I) e (II) :
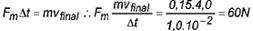
Princípio da Conservação do Momento Linear
a) Um dos mais relevantes na Mecânica; pode ser assim enunciado:
b) Num sistema físico isolado de forças externas (aquele em que a resultante das forças externas que nele agem é nula), o momento linear total permanece constante. Então:
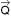
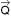
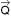
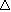
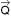
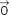
Aplicação
Antônio (um pescador do Cambixe) está com sua canoa no lago dos Reis. Inicialmente, tanto a canoa como o pescador repousam em relação à água que, por sua vez, não apresenta qualquer movimento em relação à Terra. Atritos da canoa com a água são desprezíveis e, no local, não há ventos. Num determinado instante, o pescador atira horizontalmente a sua zagaia de massa 2,0kg que sai com velocidade de 10m/s. Calcule o módulo da velocidade do conjunto pescador/canoa, de massa igual a 150kg, imediatamente após o disparo.
Solução:
Sendo o sistema fisicamente isolado:
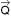
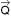
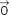
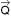
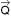
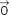
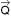
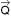
Em módulo:
Qzagaia = Qconjunto
mzagaiavzagaia = mconjuntovconjunto
2,0.10 = 150vconjunto
vconjunto = 0,13m/s