Aplicação
Um corpo movimenta-se por 10m sobre uma superfície horizontal sob a ação das forças constantes indicadas na figura. Calcule o trabalho de cada uma das forças atuantes no corpo. Dados: P = 100N; F = 50N; Fat = 10N; cos 60o = 0,5; cos 90o = 0; cos 180o = -1.
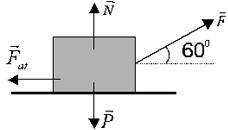
Solução:
a) 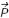
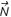
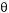
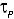
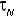
b) Trabalho de 
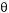
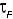
c) Trabalho de
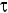
Energia Mecânica – Soma das energias cinética e potencial: Em = Ec + Ep
Energia Cinética – Energia associada ao movimento. É uma grandeza escalar que depende da massa e do quadrado da velocidade do corpo:
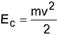
Energia Potencial – Energia armazenada associada à posição do corpo; pode permanecer armazenada indefinidamente, ou ser utilizada a qualquer momento na produção de movimento, ou seja, pode ser transformada, no todo ou em parte, em energia cinética:
Ep = mgh
Teorema da Energia Cinética – O trabalho da força resultante é igual à variação de energia cinética: 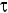
Princípio da Conservação da Energia Mecânica Durante a queda de um corpo, na ausência de forças dissipativas (como o atrito do ar), a energia potencial transforma-se em energia cinética, conservando-se a energia total do sistema.
Aplicação
Uma pedra de 2kg é abandonada de uma altura de 8m em relação ao solo. Calcule a energia cinética e a velocidade de que estará dotada a pedra ao atingir o solo? (Despreze a resistência do ar e considere g = 10m/s2).
Solução:
a) Ec = Ep Ec = mgh = 2 . 10 . 8 = 160J (ao atingir o solo, a pedra terá uma energia cinética que corresponde à energia potencial que tinha quando iniciou a queda).
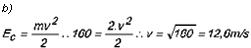
IMPULSO E MOMENTO LINEAR
Um corpo recebe um IMPULSO (
Impulso de uma força constante:
a) É uma grandeza vetorial (possui módulo, direção e sentido).
b) Tem módulo proporcional ao módulo de
c) Tem sempre direção e sentido iguais aos de