PROPRIEDADES DAS PROGRESSÕES ARITMÉTICAS
1.a propriedade (termos eqüidistantes dos extremos)
Numa P.A. finita, de dois termos eqüidistantes dos extremos é igual à soma dos extremos.
Exemplo:
Seja a P. A. (8, 10, 12, 14, 16). Observa-se que:
Os termos a2 = 10 e a4 = 14 estão eqüidistantes dos extremos a1 e a5, respectivamente.
Note que: 10 + 14 = 8 +16 = 24 .
2.a propriedade
Numa P.A. com número ímpar de termos, o termo médio é igual à média aritmética entre os extremos.
Exemplo:
Na P. A. (2, 4, 6, 8, 10), temos:
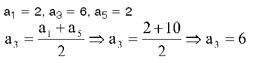
3.a propriedade
A seqüência (a, b, c) é P.A. se, e somente se, o termo médio é igual à média aritmética entre a e c, isto é:
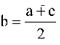
FÓRMULA DA SOMA DOS N TERMOS DE UMA P. A. FINITA
A soma dos termos de uma P. A. limitada é igual ao produto da semi-soma dos termos extremos pelo número de termos.
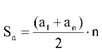
Em que:
a1 é o primeiro termo;
an é o enésimo termo;
n é o número de termos;
Sn é a soma dos n termos.
Aplicação
Achar a soma dos 8 primeiros termos da P. A. (4, 7…).
Solução:
No problema, temos a1 = 4, r = 3 e n = 8.
1.º passo (cálculo de a8)
an = a1 + (n – 1) . r
a8 = 4 + (8 – 1).3
a8 = 25
2.º passo (cálculo de S8)