Escalonamento do Sistema:

Para escalonar um sistema seguem-se passos:

a) Coloca-se como primeira equação do sistema uma equação com coeficiente da primeira incógnita igual a 1.

b) Elimina-se a primeira incógnita de todas as equações, a partir da segunda equação.

c) Deixa-se de lado a primeira equação e repetem-se os passos anteriores para as demais equações.

Exemplo:

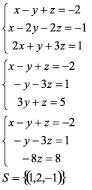
Se durante o escalonamento surgir uma equação do tipo:

0x1 + 0x2 + … + 0xn = b

a) Se b = 0: eliminamos a equação e continuamos o escalonamento.

b) Se b 0: conclui-se de imediato que o sistema é impossível.

Classificação do sistema pelo método do escalonamento.

Seja um sistema escalonado de m equações e n incógnitas.

m = n: sistema possível determinado.

Se durante o escalonamento surgir uma equação do tipo:

I. 0x1 + 0x2 + … + 0xn = b, com b 0, então o sistema é impossível.

II. 0x1 + 0x2 + … + 0xn = 0 e não ocorrer o caso anterior, então o sistema é possível e indeterminado.

Sistemas Lineares com Parâmetros

São sistemas condicionados a parâmetros inseridos em seus coeficientes.

A discussão pode ser feita por escalonamento.

Aplicação

Discutir o sistema em função dos parâmetros a e b.

Se b = 3, então o sistema é possível indeterminado.

Se b 3, então o sistema é impossível.