4. Sistema normal
Definição
Quando o determinante do sistema for diferente de zero (D ≠ 0) o sistema linear de n equações a n incógnitas será normal.
Teorema de Cramer

Veja a demonstração:
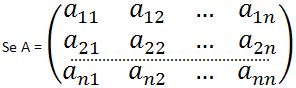

O que garante a existência e a unicidade da matriz A-1 é a condição det A ≠ 0, sendo assim, a matriz X = A-1 . B existe e é única. Portanto, o sistema normal é possível e determinado, pois admite apenas uma seqüência ordenada de n elementos (x1, x2, x3, …, xn) como a solução.
Regra de Cramer
É um método prático também usado para resolver um sistema normal.
A solução (x1, x2, x3, …, xn) que existe e é única, de um sistema normal é definida por:

Sendo que:
D ≠ 0 é o determinante do sistema.
Dj é o determinante da matriz que é obtida da matriz incompleta, quando se faz a substituição da coluna a1j, a2j, a3j, …, anj pela b1, b2, b3, …, bn, respectivamente.