5. Características de uma matriz
Para questionar um sistema podemos usar o Teorema Rouché-Capelli, que utiliza o conceito de característica de uma matriz que será chamado de determinante de ordem p.
Definição
Uma matriz M não nula é caracterizada pela máxima ordem dos determinantes não todos nulos que podem ser retirados de M. Ou seja, a característica de M é o número natural p ≥1 somente quando:
a) pelo menos um determinante for de ordem p diferente de zero.
b) todos os determinantes de ordem maior do que p forem nulos.
Exemplo:

Dada a matriz acima podemos retirar determinantes de ordem 1, ordem 2 e ordem 3, portanto essa matriz é caracterizada por 1, 2 ou 3. Veja que pelo menos um determinante de ordem 2 será diferente de zero:
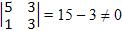
Veja abaixo todos os determinantes de ordem 3:
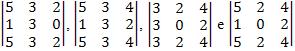
Note que a primeira e a terceira linha são iguais por isso os determinantes de ordem 3 são iguais a zero.
Portanto, a característica da matriz M é 2.
Propriedades
Não existe modificação na característica da matriz quando:
1) duas filas paralelas são trocadas.
2) as linhas são trocadas ordenadamente pelas colunas.
3) uma fila é multiplicada por uma constante k ≠ 0.
4) filas nulas são acrescentadas ou extraídas.
5) adicionamos a uma fila uma combinação linear de filas paralelas.
6) uma fila que é combinação linear das demais é eliminada.
Como calcular a característica
1) Através da propriedades podemos eliminar algumas filas, facilitando o cálculo da característica.
Exemplo:
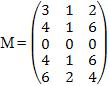
Na matriz acima todos os determinantes de ordem 3 são nulos, portanto, ao calcular a característica de M podemos eliminar esta linha.
Portanto, a característica de M será igual á da matriz
Considerando esta matriz podemos eliminar os determinantes de ordem 2, pois a segunda e a terceira linha são iguais. Portanto, a característica de N é igual à da matriz
Nesta matriz todos os determinantes de ordem 3 são nulos, pois a terceira linha é o dobro da primeira. Portanto, a característica de P é igual à da matriz
Sendo assim a característica de Q é 2, pois há pelos menos um determinante de ordem 2 diferente de zero.
Conclusão: a característica da matriz M é 2.
Teorema de Kronecker
Através do Teorema de Kronecker podemos calcular a característica de uma matriz de uma maneira mais prática.
A característica de uma matriz é p, somente quando:
1) Houver um determinante de ordem p (Dp) diferente de zero.
2) Forem nulos todos os determinantes de ordem p + 1 que podem ser obtidos orlando-se Dp, com uma das restantes linhas e uma das restantes colunas.