Projeções ortogonais
Projeções de um ponto
Chamamos a projeção ortogonal de um ponto num plano de “pé da perpendicular” ao plano pelo ponto.
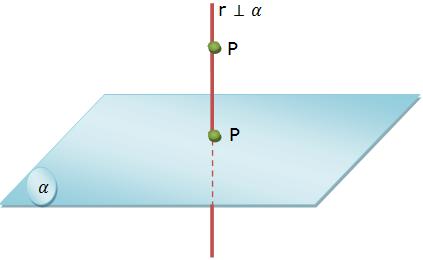
P é o ponto considerado a projeção ortogonal de P em α. Assim, denominamos ponto α de plano de projeção e a reta perpendicular r de reta projetante.
Projeção de uma figura
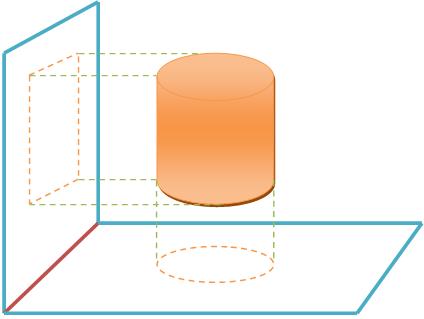
O agrupamento das projeções ortogonais dos pontos da figura é a projeção ortogonal da mesma num plano.
Vejamos o modelo:
Na figura, o retângulo é a projeção ortogonal do cilindro num plano paralelo ao eixo. Já o círculo é a projeção do mesmo cilindro num plano paralelo a base. Assim:
Projeção de uma reta
A projeção ortogonal de uma reta num plano é a união das projeções ortogonais dos pontos da reta neste plano.
I) Uma vez que a reta for perpendicular ao plano, a sua projeção ortogonal será um ponto.
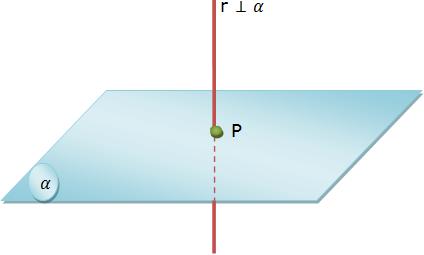
Na imagem, P forma a projeção ortogonal de r em α
II) Caso a reta não seja perpendicular ao plano, a sua projeção ortogonal projeção ortogonal será outra reta.
Na imagem, r forma projeção ortogonal de r em α.
Ângulo entre reta e plano
Uma vez que reta for perpendicular a um plano, o ângulo entre eles será reto. Assim, caso a reta seja obliqua em comparação ao plano, o ângulo entre eles será o ângulo que ela formará com sua projeção ortogonal. Desta forma:
Na imagem, obtemos:
A reta s estabelece ângulo reto com α.
O ângulo θ que a reta r estabelece com o plano α é o ângulo que a reta r estabelece com sua projeção ortogonal r’.
Retas de maior declive
Denominamos retas de maior declive de um plano α em comparação a um plano β às retas de α que constituem o maior ângulo existente com β. Comprova-se assim que os dois planos são secantes as retas de maior declive de um em relação ao outro são perpendiculares à intersecção.
Na imagem, r forma uma reta de maior declive de α em comparação a β.
Ângulo entre planos
O ângulo entre dois planos é o ângulo que uma reta de maior declive de um forma com o outro.
Na imagem:
r representa uma reta de maior declive de α em comparação a β.
r’ representa a projeção ortogonal da reta r em β.
θ representa o ângulo entre α e β.