Paralelismo
Transitividade no paralelismo
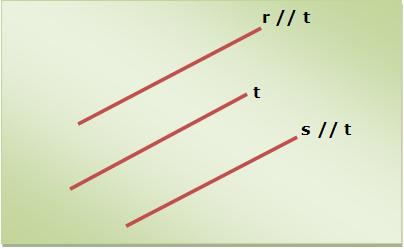
Se dissermos que duas retas são paralelas a uma terceira, elas assim serão consideradas paralelas entre si.
Vejamos a figura:
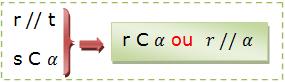
Teorema fundamental do paralelismo
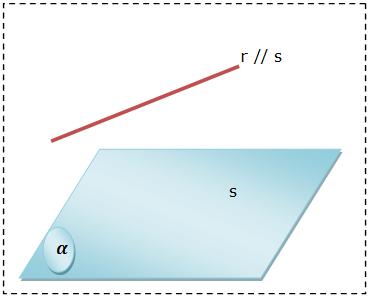
O principal requisito para que uma reta seja paralela a um plano é que de modo algum ela esteja inclusa nele e seja paralela a uma reta desse plano. Vejamos:
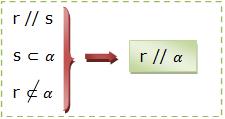
Conseqüências
a) Consideremos duas paralelas distintas, todo e qualquer plano que possui uma é paralelo ou possui a outra. Vejamos a figura:
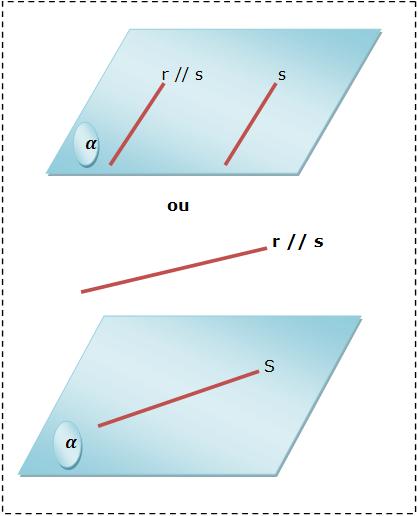
b) Ao notarmos que uma reta é paralela a um plano, podemos afirmar que toda e qualquer reta paralela a ela que tenha um ponto uniforme com o plano estará contida nele.
Vejamos:
c) Se considerarmos que uma reta é paralela a dois planos secantes, então poderemos dizer que ela é também paralela a intersecção dos dois planos. Vejamos a figura:
Note que o recíproco não é real, pois ela pode estar contida nos planos.
Teorema fundamental do paralelismo do plano
O principal requisito para que dois planos diferentes sejam paralelos é um deles possuir duas retas concorrentes entre si e paralelas ao outro. Vejamos:
Propriedade de paralelismo de planos
a) Ao possuir dois planos paralelos cortados por um terceiro, teremos intersecções paralelas.
b) Se considerarmos um ponto que não pertence a um plano, notaremos que haverá e será exclusivo o plano paralelo a ele (extensão do postulado de Euclides da Geometria Plana).
c) Teorema de Tales
Um feixe de planos paralelos determina a cerca de duas transversais secções congruentes devidamente proporcionais.