Relações métricas nos triângulos retângulos 
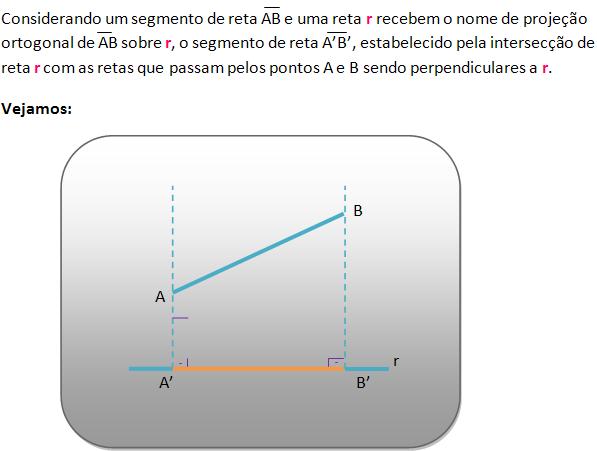
Projeção ortogonal de segmentos: 

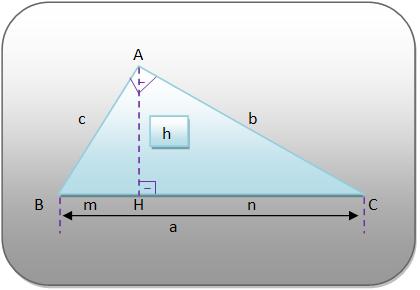
Elementos de um triângulo retângulo 
No triângulo retângulo ABC da figura acima, temos: 

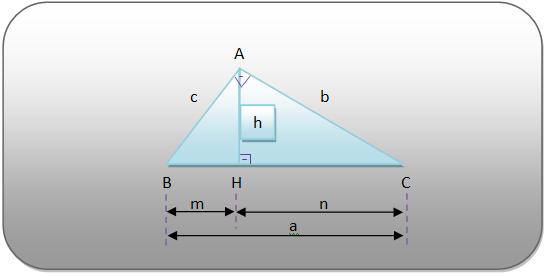
Relações métricas num triângulo retângulo

Vejamos: 

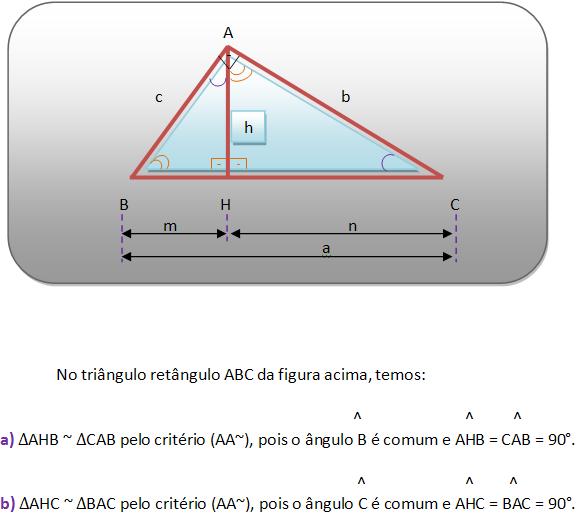
Relações das semelhanças dos triângulos:

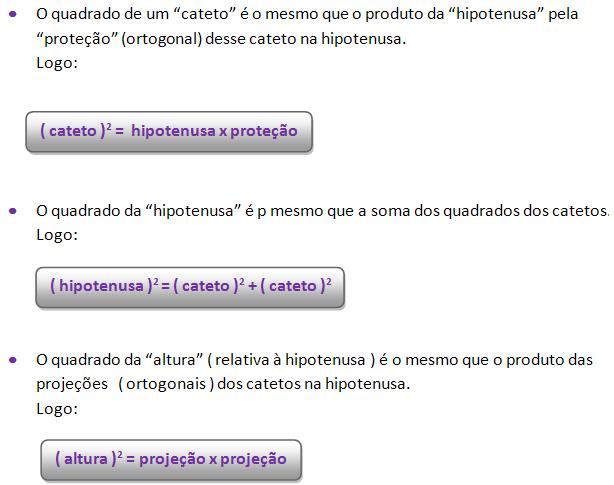
1) Através da relação de Euclides, podemos dizer que o quadrado da medida de um cateto, é o mesmo que o produto da medida da hipotenusa através da medida da projeção ortogonal deste mesmo cateto sobre a hipotenusa. 

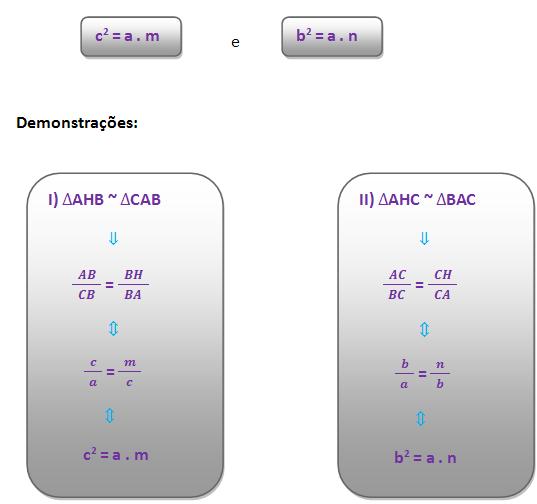
2) Através do Teorema de Pitágoras, podemos dizer que o quadrado da medida da hipotenusa, é o mesmo que a soma dos quadrados das medidas dos catetos. 

Logo, temos: 

3) Há uma igualdade entre o quadrado da medida da altura relativa e o produto das medidas das projeções dos catetos sobre a hipotenusa. 

Logo, temos: 

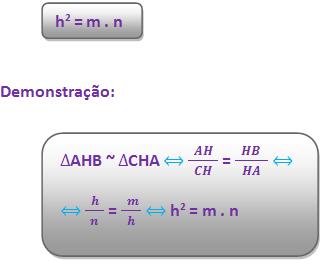
4) O produto da medida da hipotenusa pela medida da altura relativa à hipotenusa será igual ao produto das medidas dos catetos. 

Logo, temos: 

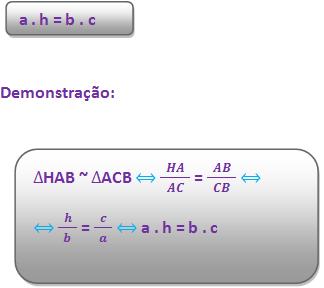
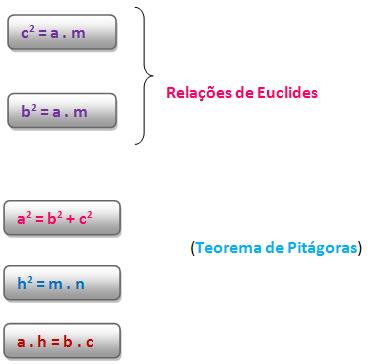
Resumo das relações métricas no triângulo retângulo 
No triângulo retângulo ABC da figura, onde BC = a, AC = b; AB = c; AH = h; BH = m e CH = n, valem as seguintes relações, vejamos: