Grandezas proporcionais

4. Grandezas proporcionais

A representação A = (a₁, a₂, a₃, …) indica que a₁, a₂, a₃, … são valores assumidos pela grandeza A. 

Quando escrevemos num determinado problema que A = (a₁, a₂, a₃, …) e B = (a₁, a₂, a₃, …), significa que quando a grandeza A assumir o valor a₁, a grandeza B também assumirá o valor b₁. 

Portanto, significa que a₁ e b₁ são valores correspondentes das grandezas A e B. Podemos dizer que a₂ e b₂ são valores correspondentes, bem como a₃ e b₃, e assim por diante. 

Grandezas diretamente proporcionais (GDP)

Considere duas grandezas A e B. A será diretamente proporcional a grandeza B somente quando os valores A e os correspondentes valores de B forem iguais. Sendo assim, quando A = (a₁, a₂, a₃, …) e B = (a₁, a₂, a₃, …) forem grandezas diretamente proporcionais, temos: 

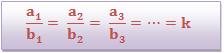
Onde k é a constante da proporcionalidade.

Exemplo:

Um ônibus percorre:

90 km em 1 hora
180 km em 2 horas
270 km em 3 horas

Portanto, neste caso, a distância e o tempo são grandezas diretamente proporcionais. 

Grandezas inversamente proporcionais (GIP)

Considere duas grandezas A e B. A será inversamente proporcional a grandeza B somente quando os produtos entre os valores A e os correspondentes de B forem iguais. Sendo assim, quando A = (a₁, a₂, a₃, …) e B = (a₁, a₂, a₃, …) forem grandezas inversamente proporcionais, temos: 

Onde k é a constante da proporcionalidade.

Exemplo:

Um ônibus percorre:

120 km em 1 hora
60 km em 2 horas
40 km em 3 horas

Portanto, neste caso, a distância e o tempo são grandezas inversamente proporcionais.