Propriedades das Progressões Geométricas

1.ª propriedade

Numa P.G. com número ímpar de termos, o quadrado do termo médio é igual ao produto dos extremos.

Exemplo:

Na PG (3, 6, 12), temos:

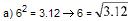
2.ª propriedade

O produto dos termos eqüidistantes dos extremos de uma P.G. é igual ao produto desses extremos.

Exemplo:

Na P.G. (4, 8, 16, 32, 64), temos:

4.64 = 8.32 = 256

3.ª propriedade

A seqüência (a, b, c), com a 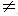0, se, e somente se, o quadrado do termo médio é igual ao produto dos extremos, isto é, b² = ac.

SOMA DOS TERMOS DE UMA P.G. FINITA

A soma dos termos de uma progressão geométrica de n termos é dada por:

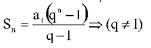
Observação – Para uma P. G. constante (q = 1), a soma dos n termos é dada por: S_n = n . a₁

Aplicações

01. Calcule a soma dos 6 primeiros termos da P.G. (1, 3, 9, 27, 81…). 

SOMA DOS TERMOS DE UMA P.G. INFINITA

Neste tópico, observaremos que para um número infinito de termos, o último termo tenderá a se anular.

A soma dos infinitos termos dessa P. G. é dada por:

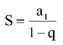
Aplicação

Calcule a soma dos termos da P. G. (2, 1, 1/2, 1/4…).

Solução:

Temos: a1 = 2 , q = 1/2

A soma dos termos dessa P. G. infinita é: 

Pela Web