Valor numérico

2. Valor Numérico

Considerando a função polinomial:

P(x) = a₀ . xⁿ + a₁ . x^n-1 + a₂ . x^n-2 + … + a_n-1 . x + a_n 
chamamos de valor numérico de P para x = α o número P(α) = a₀ . αⁿ + a₁ . α^n-1 + a₂ . α^n-2 + … + a_n-1 . α + a_n
Portanto, o valor numérico de P(α) é a imagem de α por P.

Exemplo:

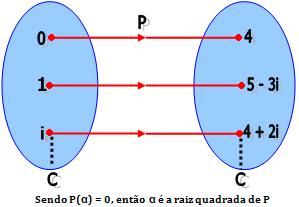
P(x) = x³ – 3ix² + 4
P(0) = 0³ – 3i . 0² + 4 = 4
P(1) = 1³ – 3i . 1² + 4 = 5 – 3i
P(i) = i³ – 3i . i² + 4 = 4 + 2i