6. Função Polinomial identicamente nula

Definição

A função polinomial será denominada nula quando um número P for caracterizado igual a 0.

Veja a representação:

P(x) ≡ 0 ⇔ P(x) = 0 ∀x ∈ C 

Teorema 

Para que a função polinomial se torne identicamente nula é indispensável que P e seus coeficientes sejam nulos.

P(x) ≡ 0 ⇔ a0 = a1 = a2 = … = an = 0 

Demonstração: 

1) a0 = a1 = a2 = … = an = 0 ⇒ P(x) ≡ 0 

Logo:

a0 = a1 = a2 = … = an = 0 ⇒

⇒ P(x) = 0 xn + 0 . xn-1 + 0 . xn-2 + … + 0 . x + 0 ⇒

⇒ P(x) = 0 + 0 + 0 + … + 0 = 0, ∀x ⇒ P(x) ≡ 0 

2) P(x) ≡ ⇒ a0 = a1 = a2 = … = an-1 = an = 0

Logo:

P(x) ≡ 0 ⇒ P(x) = 0, ∀x ∈ C ⇒

P(x0) = P(x1) = P(x2) = … = P(xn) = 0 

Onde x0, x1, x2, …, xn são números complexos dois a dois distintos, podendo ser representado pelo sistema abaixo: 

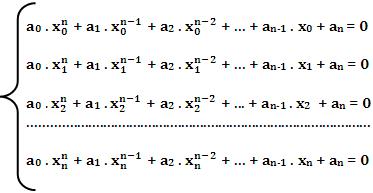
Este sistema é linear homogêneo, com n + 1 equações nas n + 1 incógnitas a0, a1, a2, …, an-1, an.

Note que: 

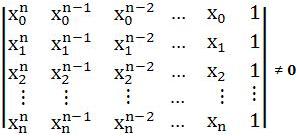
Nesse caso, é um determinante de Vandermonde com os elementos característicos dois a dois distintos, conseqüentemente este sistema aceita apenas a solução trival, pois:

a0 = a1 = a2 = … = an-1 = an = 0