Divisão por (x – α) . (x – β)

11. Divisão por (x – α). (x – β)

Considerando A(x) divisível por (x . α) . (x . β), nesse caso podemos realizar duas divisões contínuas para obter o quociente, através do Dispositivo Prático de Briot-Ruffini. 

Veja a representação:

Quando A(x) não for divisível por (x . α) . (x . β), devemos utilizar o Método da Chave ou o Método de Descartes para obter o quociente e o resto.

Questão

Considerando os restos r₁ e r₂ das divisões da função polinomial A por x – α e x – β, respectivamente, sendo α ≠ β, determine o resto da divisão de A por (x – α) . (x – β).

Resolução

1) Pelo enunciado temos: 

2) Sabemos que gr(B) = 2, portanto o resto da divisão de A por (x – α) . (x – β) é do tipo R(x) = ax + b.

3) Da definição de divisão temos: 

4) De (III), para x = α e x = β, temos:

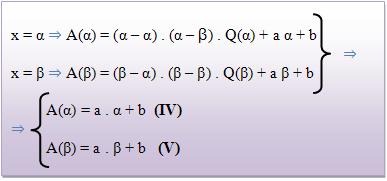
5) Fazendo a substituição (I) e (II) em (IV) e (V), temos:

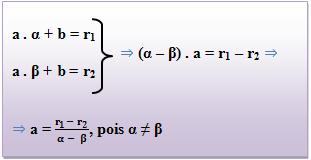
6) Fazendo a substituição do valor de a em a . α + b = r₁, origina:

7) Conclusão: O resto da divisão de A por (x – α) . (x – β), sendo α ≠ β, é: