12. Representação geométrica dos números complexos
Plano de Argand Gauss
O conjunto C também pode ser representado pelos pontos do Plano Cartesiano ou Plano de Argand Gauss.
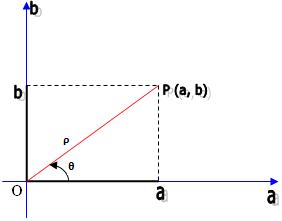
Considere um sistema de coordenadas cartesianas ortogonais xOy e um ponto P de coordenadas (a, b) num Plano Cartesiano ou Plano de Argand Gauss. Sabendo que c = (a, b) = a + bi, chegamos à conclusão de que há uma relação biunívoca entre os pontos do plano e os números complexos.
Ponto P: imagem geométrica de c ou o afixo de c.
Eixo das abscissas Ox: eixo real, uma vez que seus pontos são os afixos dos números reais.
Eixo das ordenadas Oy: eixo imaginário, uma vez que seus pontos são os afixos dos números imaginários puros.
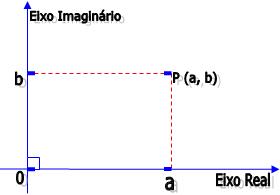
Interpretação geométrica
1) O módulo ρ simboliza a distância entre os ponto P e O, pois conforme o teorema de Pitágoras temos:
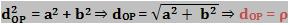
2) O argumento θ simboliza a medida do ângulo constituído por 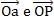
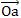
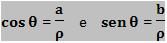
3) Representando o complexo c na forma algébrica fazemos uma referência ao ponto P dado pelas suas coordenadas polares.
c = a + bi ⇔ P(a, b)
4) Representando o complexo c na forma trigonométrica fazemos uma referencia ao ponto P dado pelas coordenadas polares.
c = ρ (cos θ + i . sen θ) ⇔ P(ρ, θ)