Operações na forma trigonométrica

Por Redação
31/05/2012 às 17:48

13. Operações na forma trigonométrica

Multiplicação

1) Considere c₁ = ρ₁ (cos θ₁+ i . sen θ₁) ≠ 0 e c₂= ρ₂ (cos θ₂ + i . sen θ₂) ≠ 0

Logo:

c₁. c₂ = [ρ₁(cos θ₁ + i . sen θ₁)] . [(ρ₂ (cos θ₂ + i . sen θ₂)] ⇔

⇔ c₁ . c₂= (ρ₁ . ρ₂) . [(cos θ₁ . cos θ₂ – sen θ₁ . sen θ₂) + i(sen θ₁ . cos θ₂ + sen θ₂ . cos θ₁)] ⇔

⇔ c₁ . c₂ = (ρ₁ . ρ₂) . [cos (θ₁ + θ₂) + i . sen (θ₁ + θ₂)] pois

2) Conclusão: o módulo do produto é o produto dos módulos e o argumento do produto é a primeira determinação positiva ou nula da soma dos argumentos.

3) Veja a representação:

4) Este resultado também pode ser generalizado para n fatores. Veja:

c₁ . c₂ . c₃ . … . c_n = ( ρ₁ ρ₂ρ₃ … ρ_n) . [cos (θ₁ + θ₂ + θ₃ + … + θ_n) + i . sen (θ₁ + θ₂ + θ₃ + … + θ_n)]

Divisão

1) Considerando c₁= ρ₁ (cos θ₁ + i . sen θ₁) ≠ 0 e c₂= ρ₂ (cos θ₁ + i . sen θ₁) ≠ 0

Logo:

2) Conclusão: o módulo do quociente é o quociente dos módulos e o argumento do quociente é a primeira determinação positiva ou nula da diferença dos argumentos.

3) Veja a representação:

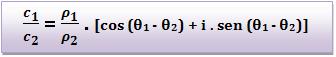
Potenciação com expoente inteiro

Considere c = ρ . (cos θ + i . sen θ) ≠ 0, nesse caso cⁿ é o produto de n fatores iguais a c, logo:

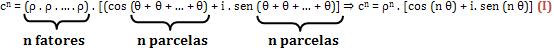
2) Expoente n = 1

c₁= c = ρ . (cos θ + i . sen θ) = ρ₁ . [cos (1 . θ) + i . sen (1 . θ)]

Nesse caso a fórmula (I) é equivalente para n = 1

3) Expoente n = 0

c₀ = 1 = 1 . (cos 0 + i . sen 0) = ρ₀ . [cos (0 . θ) + i . sen (0 . θ)]

Nesse caso a fórmula (I) é equivalente para n = 0

Considerando n < 0 logo – n > 0, sendo assim a fórmula (I) é equivalente para –n. Em vista disso:

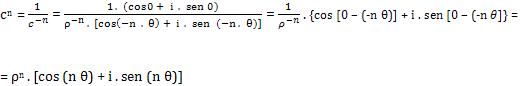
Nesse caso a fórmula (I) é equivalente para n < 0

5) Conclusão: Se c = ρ (cos θ + i . sen θ) ≠ 0 e n ∈ Z, nesse caso o módulo de cⁿ é ρⁿ e o argumento de cⁿ é a primeira determinação positiva ou nula de nθ.

6) Veja a representação:

Radiciação

1) Definição

Um número a será considerado uma raiz enésima de c somente quando elevado ao expoente n reproduzir a.

Veja a representação:

2) Raiz aritmética

Conforme a definição podemos dizer, por exemplo, que os números 4 e -4 são as raízes quadradas de 16, pois (-4)² = 4² = 16. Por isso, sabemos que o número real 4 é a raiz quadrada aritmética de 16 e é representado por . Logo, o número real negativo -4 é simbolizado por , pois ele é simétrico de 3.

Portanto:

Considerando , podemos afirmar a existência e unicidade do número positivo , denominado a raiz enésima aritmética de a.

3) Cálculo das raízes enésimas

Considere um número complexo como c = ρ(cos θ + i . sen θ) ≠ 0 e sua raiz enésima como: c_k = ρ_k(cos θ_k + i . sen θ_k).

Conforme a definição, pela fórmula de Moivre, temos:

Conclusão:

Em (I) o módulo de todas as raízes enésimas de c é

Em (I):

Portanto, só há n valores diferentes de θ_k, são eles: θ₀, θ₁, θ₂, …, θ_n-1

4) Conclusão: Todo número complexo c = ρ (cos θ + i . sen θ) ≠ 0 admite b raízes enésimas cujos módulos são todos iguais a e cujos argumentos são: