4. Forma algébrica
1) Analise o esquema abaixo:
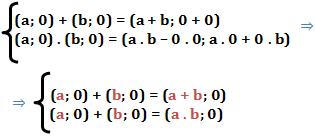
Podemos concluir que em relação à definição, quando aplicamos a adição ou a multiplicação na forma (a; 0) e (b; 0) recusamos o ( ; 0) e calculamos somente a soma ou o produto dos números reais a e b.
Sendo assim, os números complexos (a; 0) e (b; 0) são substituídos por a e b, respectivamente.
Representamos assim:
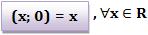
2) O número complexo (0; 1) é denominado unidade imaginária, seno simbolizado por i. O valor de i2 é -1. Sendo assim:
i2 = i . i = (0; 1) . (0; 1) = (0 – 1; 0 + 0) = (-1; 0) = -1
Logo:
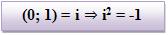
3) Os números complexos de forma (0; y) são denominados imaginários puros e são iguais a yi. Sendo assim:
y . i = (y; 0) . (0; 1) = (0 – 0; y + 0) = (0; y)
Logo:
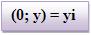
4) O número complexo z = (x; y) também pode ser representado na forma z = (x; 0) + (0; y). Considerando (x; 0) = x conforme o item (1), e (0; y) = yi conforme o item (3), logo:
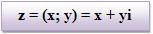
Esta é uma forma algébrica de z.