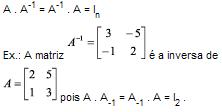Produto de um Número Real por uma Matriz

Se é um número real, o produto desse número por uma matriz A = (aij)mxn é uma matriz B = (bij)mxn tal que bij = . aij 

Propriedades do Produto de um Número por uma Matriz

Se A e B são matrizes de mesma ordem e e são números reais, valem as seguintes propriedades:

a) 1A = A

b)  . (A + B) = A +  B

c) . (b . A) = ( . b) . A

d) ( + b) . A =  . A + b . A

e) (  . A)T =  . AT

Produto de Matrizes

Dadas duas matrizes A = (aij)mxn e B = (bij)mxn, o produto da matriz A pela matriz B, nesta ordem, somente será possível quando o número de colunas da matriz A for igual ao número de linhas da matriz B. 

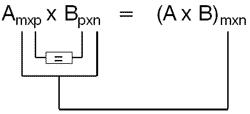
A matriz produto (A x B)mxn terá número de linhas de A e número de colunas de B.

Os elementos da matriz produto são obtidos multiplicando-se cada elemento das linhas da matriz A pelo correspondente elemento das colunas da matriz B e adicionando os produtos obtidos.

Propriedades do Produto de Matrizes
Sendo A, B, C matrizes, e a um número real, e supondo as operações abaixo possíveis, temos que:

a) A.(B.C) = (A.B).C (ASSOCIATIVA)

b) A.(B+C) = A.B + A.C (DISTRIBUTIVA À DIREITA)

c) (A+B).C = A.C+B.C (DISTRIBUTIVA À ESQUERDA)

d) 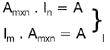I É A IDENTIDADE

e) (A . B) = A . (B) = . (A . B)

f) (A . B)T = BT . AT

Observações Importantes:

1.ª A multiplicação de matrizes não é comutativa, isto é, existem matrizes A e B tais que AB BA.

2.ª Na multiplicação de matrizes não vale o anulamento do produto, isto é, podemos ter A . B = 0 mesmo com A 0 e B 0.

3.ª Não vale também a simplificação, isto é, podemos ter AB = AC, mesmo com A 0 e B C.

Matriz Inversa

Uma matriz quadrada A de ordem n diz-se inversível ou não singular se, e somente se, existir uma matriz que indicamos por A-1, denominada inversa de A, tal que: