Operações com Matrizes

Matriz Identidade ou Matriz Unidade 

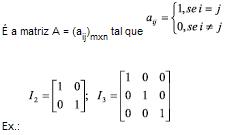
Matriz Transposta (At)

É a matriz que se obtém trocando ordenadamente as linhas pelas colunas da matriz dada.

Se B = (b_ij)_mxn é transposta de A = (a_ij)_mxn, então b_ij = a_ij.

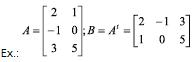
Matriz Diagonal 

É uma matriz quadrada onde a_ij = 0, para i  j, isto é, os elementos que não estão na diagonal principal são nulos.

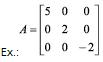
Matriz Simétrica

É uma matriz quadrada A tal que A^t = A, isto é, a^ij = a^ij para i j. 

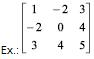
Matriz Anti-simétrica

É uma matriz quadrada A tal que A^t = -A , isto é, a_ij = -a_ij para i e j quaisquer. 

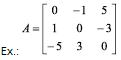
Operações com Matrizes

Igualdade de Matrizes

Duas matrizes A = (a_ij)_mxn e B = (b_ij)_mxn de mesma ordem, são iguais se, e somente se, a_ij = b_ij.

Propriedades da Igualdade

– Se A = B, então A^t = B^t

– (A^t)^t = A

Adição e subtração de Matrizes

A soma de duas matrizes A = (a_ij)_mxn e B = (b_ij)_mxn de mesma ordem é uma matriz C = (a_ij)_mxn tal que C = a_ij + b_ij.

A subtração de matrizes é dada pela sentença:

A – B = A + (– B ) 

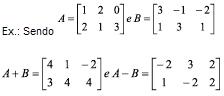
Propriedades da adição de Matrizes

a) A + B = B + A (COMUTATIVA)

b) (A + B) + C = A + (B + C) (ASSOCIATIVA)

c) A + 0 = 0 + A = A (ELEMENTO NEUTRO)

d) A + (-A) = (-A) + A = 0 (ELEMENTO OPOSTO)

e) (A + B)^T = A^T + B^T (TRANSPOSTA DA SOMA)