O Cálculo Diferencial e Integral, também conhecido como Cálculo Infinitesimal, ou apenas de Cálculo, surgiu através da Geometria e da Álgebra, e por ele podemos estudar taxas de variações de grandeza, como, por exemplo, a inclinação de uma reta, ou acumulação de quantidade, sendo volume de sólidos um exemplo desta última. Este tópico importante da matemática (tópico este que dá muita dor de cabeça para o povo das exatas) é dividido, basicamente, em 3 partes: limites, derivadas e integrais. Neste texto, falaremos sobre estas duas últimas!

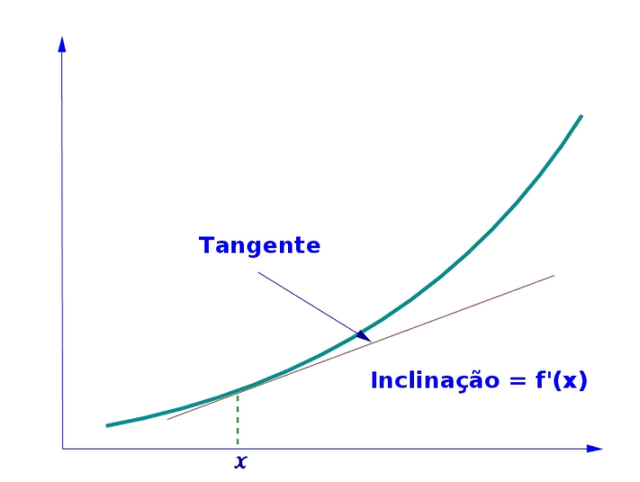
O que é Derivada?

Derivada

Para determinar uma tangente num certo ponto P, Fermat fez o seguinte: ele imaginou outro ponto Q localizado em uma curva, formando a reta PQ e fazendo-a secante em relação a esta curva. Fazendo o ponto Q “deslizar” até o ponto P, sobre tal curva, ele obteve uma reta PQ aproximada de outra reta t, reta esta que Fermat chamou de tangente em relação a curva no ponto P.

Foi observado por Fermat que, em certas funções, nos pontos onde a curva detinha valores extremos, a tangente ao gráfico deveria  se caracterizar como sendo uma reta do tipo horizontal,  uma vez que comparada ao valor assumido por  tal função num dos pontos P(x, f(x)) com o valor do outro ponto Q(x+E, f(x+E)) próximo de P, a diferença entre f(x+E) e f(x) era mínima, praticamente nula,quando comparada com o valor de E, diferença entre abscissas de Q e P.  Deste modo, ele relacionou  a determinação de tangentes à curvas e de extremos.

Assim nascia o conceito da derivada. Dentre muitos tópicos deste assunto (que é muito extenso, contendo a Regra da Cadeia, a Regra de L’Hopital, entre outros), falarei de como se resolve uma derivada básica:

Imagine uma função x elevada ao quadrado (x²). A derivada desta função, que leremos como f ‘(x) (função x linha), será 2x,. Por quê? Vocês concordam que f(x) = x² pode ser lido como f(x) = 1.x² (função de uma vez x²)? Então, para definir da derivada desta função, subtraímos 1 do expoente (no caso, o número 2) e multiplicaremos o número do expoente original  pelo número que esta multiplicando x, ficando, no exemplo dado: f ‘(x) = 2.1.x2+1, que é f’’(x) = 2x. Dando um outro exemplo: a derivada de f(y) = 3y5 é f ’(y) = 15y4.

Entenderam? Simples, não?

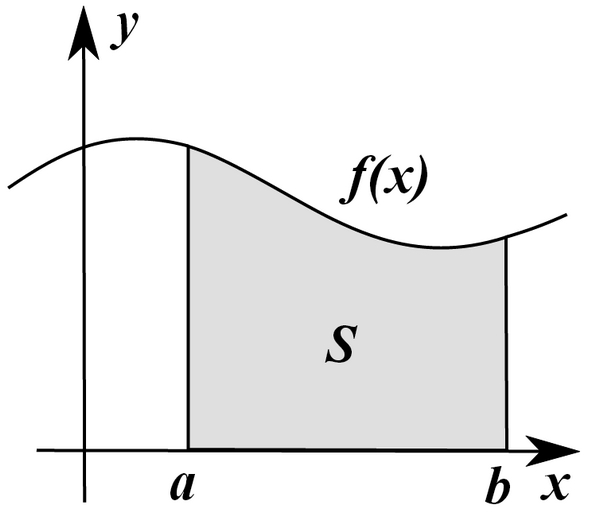
O que é Integral?

Integral

Então, agora vamos a outro tópico:  Na matemática, tudo tem seu inverso. Apenas para dar alguns exemplos: o inverso do seno é cossecante (cossec), o inverso de tangente é cotangente, o inverso de adição é subtração e o inverso de multiplicação é divisão. A derivada também tem sua inversa, que  é chamada de antiderivada ou integral. A integral pode ser definida ou indefinida, e dentro disto também temos inúmeros tópicos (sendo necessários o cálculo II, III, IV, E.D.O., dentro de outras várias matérias, só para explicar isto).  A integral é representada por  ∫.

Vou falar aqui apenas da integral indefinida. Imagine f ’(x) = 2x. A integral desta função é representada por g(x) = ∫2x dx. Para definir esta integral, somaremos 1 ao expoente da função e dividiremos tal função pelo resultado desta soma. Explicando na prática: g(x) = ∫2x dx =  =  = x². Outro exemplo de integral é g(x) = ∫2x + 5 dx = x² + 5.

Nos dois exemplos dados acima, observamos que tanto x² quanto x² + 5 são integrais indefinidas para 2x. Estas funções são denominadas de integrais primitivas, e a diferença entre elas é sempre uma constante. Ou seja: a integral indefinida de 2x é x² + C, onde C é uma constante real.