Para quem ainda não conhece, Isaac Newton foi um físico e matemático inglês, muito famoso por ter sido o primeiro cientista a identificar o que se entende hoje por Lei da Gravidade.
Newton fez uma série de outras contribuições importantes, em diversos campos da ciência, como a matemática, a física, a astronomia e até mesmo a alquimia, que era um de seus maiores interesses.
Newton ficou para a posteridade por causa da Lei da Gravidade, como já dito, mas também é lembrado por uma série de outras contribuições e estudos, sendo que os mais curiosos remetem à alquimia, que foi citada anteriormente como sendo um de seus maiores interesses.
Além da alquimia, outro grande interesse de Newton era a matemática, que foi objeto de muitos de seus principais estudos, e algumas de suas citações são lembradas e reverenciadas até os dias de hoje como sendo obras de um gênio.
E o mais curioso é que uma dessas contribuições que lhe é atribuída, na verdade sequer foi criada por ele, mas sim, foi criada a partir de alguns de seus estudos e contribuições.
Pois é sobre essa suposta contribuição, que figura no meio de suas contribuições à matemática que falaremos nesse artigo, o famoso binômio de Newton, que é muito utilizado dentro da matemática moderna e representa uma de suas contribuições mais notáveis.
Por isso, vamos entender um pouco mais sobre o seu funcionamento, para que seja possível entender também como enxergava a matemática esse que é um dos maiores gênios que o mundo já conheceu.
Resumo:
O que é binômio de Newton?
O binômio de Newton nada mais é do que um estudo complementar para o que se entende por estudo do produto notável.
Sua criação, na verdade, não se deu necessariamente pelos estudos de Isaac Newton, mas por causa de alguns de seus estudos matemáticos preliminares, e por isso acabou ganhando seu nome.
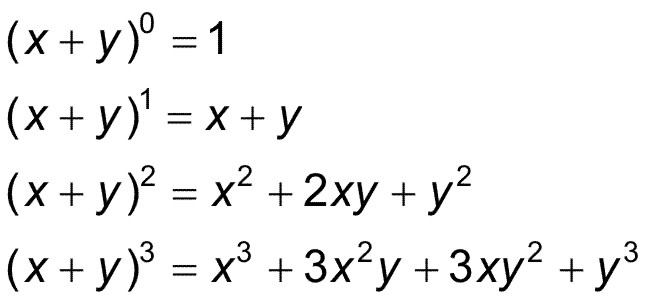
Funcionamento do binômio de Newton
O funcionamento do binômio de Newton é bastante simples, sendo que se dá, em linhas gerais, da seguinte forma:
- O produto notável determina que um binômio elevado ao quadrado será igual ao quadrado do primeiro monômio mais duas vezes o primeiro, vezes o segundo monômio mais o quadrado do segundo monômio.
Sua aplicação é fundamental para quem deseja entender melhor algumas das principais operações da matemática moderna.
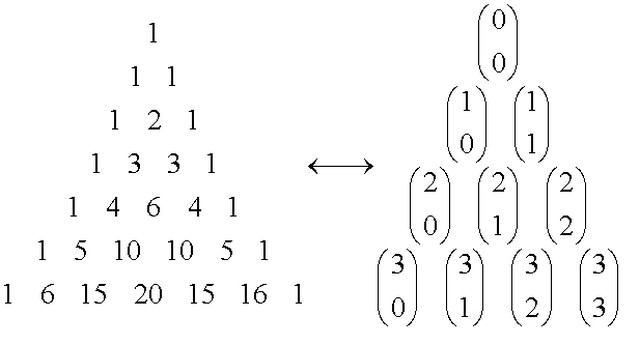
O binômio de Newton possui uma fórmula, que se baseia no principio citado anteriormente, mas há também variações de operações relacionadas a ele, como o triangulo de Pascal e o teorema do binômio de Newton.