A potenciação facilita a vida do homem quando o assunto é simplificar os cálculos para se chegar ao resultado de uma operação. Ela possui suas propriedades, como vimos anteriormente. Agora vamos estudar alguns casos especiais: potência de expoente 1, potência de expoente zero e multiplicação de potência de mesmo expoente.

Potência de expoente 1

Podemos definir a potência de expoente 1, quando a base (qualquer número natural) elevada ao expoente  1  resultará sempre na própria base. Resumidamente, toda a potência em que o expoente for 1, o resultado é igual a base. Assim, a¹ = a. Exemplo: 3¹ = 3; 18¹ = 18; 596¹ = 596.

Potência de expoente zero (0)

Podemos definir a potência de expoente zero (0), quando a base (qualquer número natural) elevada ao expoente zero resulta em 1. Portanto, toda a potência de expoente zero o resultado é igual a 1. Assim, a⁰ = 1. Exemplo: 3⁰ = 1; 25⁰ = 1; 194⁰ = 1.

Multiplicação de potência de mesmo expoente

Podemos definir o produto de potência de mesmo expoente, quando multiplicamos potências de mesmo expoente, com bases diferentes, em que preservamos e multiplicamos as bases. Assim, aⁿ. bⁿ = (a . b)ⁿ. Exemplo: 2² . 4² = (2 . 4)² =  8²

Radiciação – operação inversa da potenciação

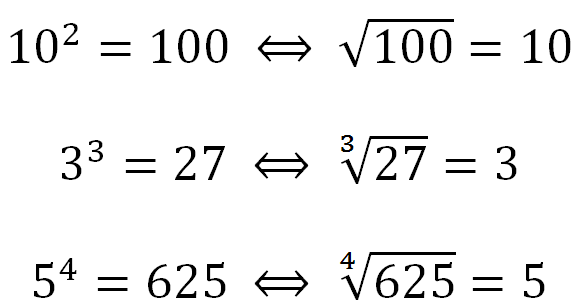
Para entendermos melhor o que é radiciação, vamos esclarecer um pouco sobre a história. A origem da palavra radical vem do latim radix que significa raiz.

Símbolo da raiz quadrada

Na matemática, o símbolo criado para definir a ideia de raiz é  √¯ . Não sabemos ao certo quais dos povos antigos utilizou-o primeiro para a prática em operações de matemática. É sabido que alguns atribuem a criação do mesmo aos árabes, outros entendem que os primeiros registros são oriundos dos povos Hindus e mais tarde chegaria aos povos da Grécia. Em torno do século XVII, o símbolo  já era bastante utilizado.

Sendo assim, para indicarmos o quadrado de um número natural utilizamos o símbolo ²√¯ , ou apenas √¯ . Podemos ler como: a raiz quadrada de um número natural. Exemplo: ²√¯ 25 = 5, então 5² = 25.

Nomenclatura

²√¯ 25  = 5  –  O número 2 é denominado de índice, o número 25 é o radicando e o número 5 é a raiz quadrada.

Exercícios

1)      Calcule a raiz quadrada dos números abaixo:

a) √¯ 4

b) √¯ 169

c) √¯ 144

d) √¯ 9

e)  √¯ 0

Boa sorte!