Resumo:
Critérios de divisibilidade
Conhecer os critérios de divisibilidade facilita a resolução de cálculos envolvendo divisões. Vejamos alguns critérios de divisibilidade:
- Divisibilidade por 2: Um número é divisível por 2, quando o algarismo das unidades for 0, 2 , 4, 6 ou 8. Um número que é divisível por 2 é denominado par, caso contrário, ímpar.
- Divisibilidade por 3: Um número é divisível por 3, quando a soma dos valores absolutos de seus algarismos for divisível por 3.
- Divisibilidade por 4: Um número é divisível por 4, quando o número formado pelos dois últimos algarismos da direita for 00 ou divisível por 4.
- Divisibilidade por 5: Um número é divisível por 5, quando o algarismo das unidades for 0 ou 5.
- Divisibilidade por 6: Um número é divisível por 6, quando for divisível por 2 e por 3 simultaneamente.
- Divisibilidade por 10: Um número é divisível por 10, quando o algarismo das unidades for 0 ( zero )
Número de Divisores
O conjunto dos divisores de um número natural x é o conjunto D(x) formado por todos os números naturais que são divisores de x.
Exemplo: o conjunto dos divisores de 36.
D(36) = { 1, 2, 3, 4, 6, 9, 12, 18, 36}
Roteiro para obter todos os divisores naturais de um número
(vamos utilizar o 36 como exemplo)
1º) fatoramos o número
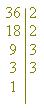
2º) colocamos um traço vertical ao lado dos fatores primos
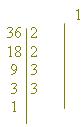
3º) na linha de cada fator primo vamos colocando os produtos dele pelos números já colocados nas linhas de cima.
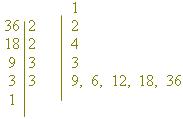
D(36) = { 1, 2 , 3, 4, 6, 9, 12, 18, 36 }
Roteiro para obtermos o número de divisores naturais de um número: nD(x)
(vamos utilizar o 36 como exemplo)
1º) fatorar o número
2º) a cada expoente acrescentamos uma unidade e a seguir efetuamos o produto, resultando assim o número de divisores naturais do número
então 36 possui 9 divisores naturais
OBS: De um modo geral, o número de divisores naturais do número natural
x = an . bm . cp . …
nD(x) = ( n + 1 ) . ( m + 1 ) . ( p + 1 ) . …