Na matemática, entendemos por potenciação a forma pela qual podemos calcular multiplicações com números (fatores) iguais. O homem sentiu a necessidade de criar um método mais fácil, rápido e preciso, sem complicações e complexidade. Foi assim que surgiu à potenciação. Com ela, realizamos cálculos mais complexos de forma mais eficiente.

Na potenciação, usamos as nomenclaturas: base, para o número a ser multiplicado, e expoente, para o número de vezes que esse número irá se multiplicar, e potência, para o resultado.

Na matemática, tudo é regra, mas temos também as exceções, portanto para que todo o cálculo seja correto é preciso seguir algumas normas. Como não poderia ser diferente, a potenciação possui as suas propriedades. Vamos estudá-las, não será tão difícil! Preste atenção!

Propriedades da potenciação

Propriedades Potenciação

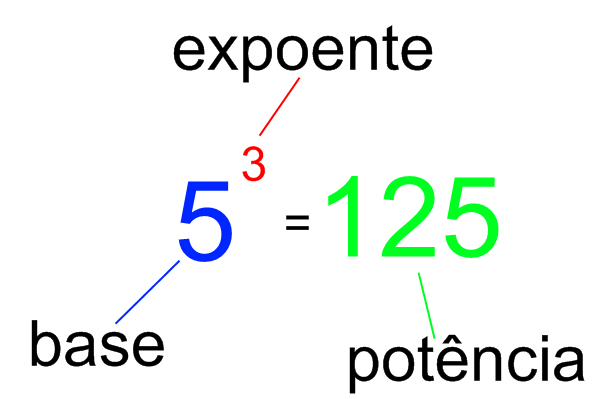
Multiplicação de potência de mesma base

Para multiplicarmos a potência de mesma base, ou seja, de mesmo número, preserva-se a mesma base e soma os expoentes. Vamos exemplificar: 2² X 2³ = 2² + ³= 5 = 25

Dessa forma, simplificamos ou reduzimos a seguinte operação: (2.2) x (2.2.2) = (2.2.2.2.2) = 25

Divisão de potência de mesma base

Para dividirmos potência de mesma base, ou seja, de mesmo número, preserva-se a mesma base e subtrai os expoentes. Nessa situação, devemos lembrar que todos os números devem ser naturais, que a base deve ser diferente de zero e o primeiro expoente deve ser maior ou igual ao segundo. Vamos exemplificar: ab : ac = ab – c, o a deve ser 0 e b c. Exemplo: 2³ : 2² = 2³-² = 2¹ = 2

Potência de potência

Ocorre quando multiplicamos uma potência à outra potência. Assim, temos uma potência de potência, e para resolvê-la preservamos a base e multiplicamos os expoentes. Exemplo: (2²)³ = 2 ² . ³ = 26

As expressões numéricas

Para resolvermos uma expressão numérica devemos seguir a seguinte regra: quando encontramos os parênteses, os colchetes e as chaves, em primeiro lugar, efetuamos as operações iniciadas entre os parênteses, em seguida as operações com colchetes e por último as operações entre as chaves.

Da mesma forma, quando as expressões indicam as adições, as subtrações, as multiplicações, as divisões e as potenciações, resolvemos primeiro as potências, depois as multiplicações e divisões, na sua ordem, e posteriormente, as adições e as subtrações na ordem da esquerda para direita.