Lançamento oblíquo
A velocidade de lançamento forma com a horizontal um ângulo distinto de 0° e de 90°.
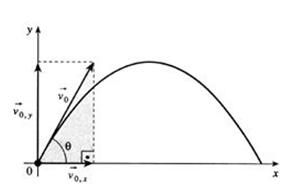
A velocidade V0 pode ser decomposta em duas componentes: Vox (componente da velocidade no eixo dos x) e Voy (componente da velocidade no eixo dos y):
Vox = Vo . cos Voy = Vo . sen
O lançamento oblíquo resulta da composição de dois movimentos independentes:
a) Movimento horizontal – Esse movimento é uniforme, uma vez que Vox é constante (desprezando-se a resistência do ar).
b) Movimento vertical – Nesse movimento, a velocidade é variável, pois o corpo está sujeito à aceleração da gravidade: na subida, o movimento é retardado (velocidade e aceleração têm sentidos contrários); na descida, o movimento é acelerado (velocidade e aceleração têm sentidos iguais).
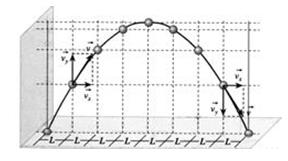
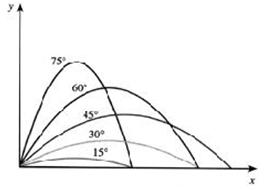
Importante: o alcance é o mesmo para diferentes corpos, lançados com a mesma velocidade inicial e com ângulos de lançamento complementares (aqueles cuja soma vale 90°).
Velocidade e aceleração no vértice da parábola
Quando falamos do ponto mais alto da trajetória, podemos dizer que a componente vertical da velocidade do projétil automaticamente irá se anular, e a velocidade irá diminuir à componente horizontal.
Vejamos a função:

Propriedades relativas ao ponto mais alto da trajetória
Existem algumas propriedades que estão relacionadas com o ponto mais alto da trajetória. Vejamos:
1- Sua componente vertical é nula, ou seja, Vy = 0.
2- Sua velocidade tem direção horizontal e apresenta um módulo igual à Vo cosα.
3- O módulo da velocidade apresenta um valor muito baixo.
4- A aceleração é composta por apenas uma componente centrípeta, ou seja, a aceleração vetorial é perpendicular a velocidade vetorial.
5- Um módulo de sua aceleração tangencial é nulo.
6 – Se o módulo da aceleração escalar for o mesmo da aceleração tangencial, a aceleração escalar será igual à zero.
Cálculo do tempo de subida e de queda
Para calcular o tempo de subida, pode-se usar apenas o movimento vertical. Vejamos:
Vy = Voy + Yy t (MUV)
Vy = Vo senα – g t
Já quando for calcular o ponto mais alto, devemos pensar que: t = ts e Vy=0, ou seja:
Quando os efeitos do ar são desprezados, o tempo da subida e o da queda são os mesmos. Vejamos:
Velocidade num ponto qualquer da trajetória
Pensando em um ponto genérico de certa trajetória, das coordenadas (x; y), devemos saber que consequentemente sua velocidade terá duas componentes:
1- A velocidade possui uma componente horizontal, que não depende do valor de x, que é a seguinte: Vx = V0 cosα.
2- A velocidade possui também uma componente vertical Vy, representada por: Vy² = V²Oy + 2yy Δsy (equação de Torricelli)
V² = V²O (senα)² – 2 g y
É importante lembrarmos que obtemos a velocidade total pela composição vetorial entre Vx e Vy.
Vejamos:
Cálculo da altura máxima
Com base nos princípios de Galileu, para se calcular a altura máxima é preciso analisar o movimento vertical. Vejamos a função para se calcular a altura máxima:
Cálculo do alcance horizontal
Com base nos princípios de Galileu, o alcance horizontal é calculado, a partir da análise do movimento horizontal. Vejamos a função para se calcular o alcance horizontal:
Notas:
* Quando V0 e g forem constantes, o seu alcance horizontal se tornará máximo, quando sen2α = 1 (lembrando que esse é o valor máximo se seno). Vejamos: