Cálculo da defasagem total de duas ondas num ponto P

No esquema abaixo, veremos dois pontos F1 e F2 que representam duas fontes que lançam ondas de freqüências iguais a f (período T=1/f) e também o comprimento da onda λ, que após percorrerem as distâncias x1 e x2, chegam ao ponto P, onde irão sofrer interferência, vejamos: 

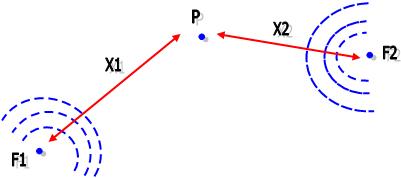
Existem fatos que explicam o porquê que as ondas ao alcançarem o ponto P podem estar defasadas, vejamos esses fatos:

(I) Defasagem inicial: ocorre quando uma fonte entra em ação primeiro que a outra. Portanto podemos concluir que caso o intervalo de tempo existente entre as partidas das ondas seja igual a um período (T), sua defasagem angular será de 2πrad. Logo, aplicaremos uma regra de três, vejamos: 

(II) Defasagem por diferença de percursos: Ocorre quando as ondas de uma fonte vão até o ponto P, com uma distância maior que a distância percorrida pelas ondas de uma outra fonte. Portanto podemos observar que caso no caminho das fontes até o ponto P, as ondas percorrerem um comprimento de onda a mais do que a outra, a defasagem angular existente entre as duas será de 2π rad. Logo aplicaremos uma regra de três, vejamos:

(III) Defasagem por reflexões com inversão de fase:  toda vez que uma das ondas em seu caminho até o ponto P sofrer uma reflexão com inversão de fase, irá acrescentar uma defasagem de π rad. Portanto:

Onde n = número de reflexões com inversão de fase.

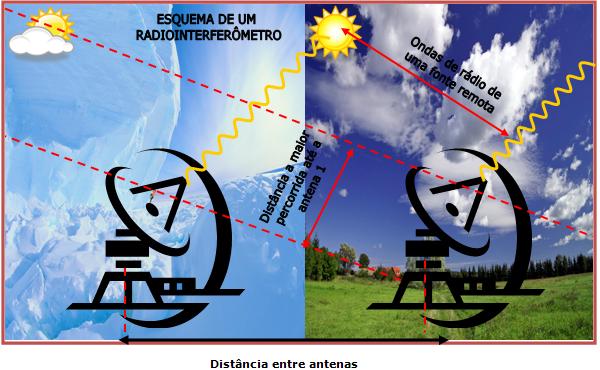
Se tivermos duas antenas de rádio colocadas à considerável distância que uma onda d rádio terá que percorrer da fonte até a primeira antena não será exatamente a mesma a mesma até a segunda antena. Dessa forma quando uma antena estiver recebendo uma crista de onda, por exemplo, a outra poderá não estar, e se combinarmos os sinais de ambas as antenas, teremos a formação de certas imagens de interferência na tela de um monitor. Pela manipulação das duas antenas e dos sinais resultantes, pode-se determinar com bastante precisão a posição de uma fonte de ondas de rádio n céu.