
Segundo alguns livros, a lógica desenvolveu-se no século XIX. Mas isto não é bem verdade. Todos nós usamos a lógica no dia a dia, às vezes sem nos darmos conta disso.
Ex: Seu pai lhe diz: se você tirar 10 em Física e Matemática, lhe darei um presente. Você sabe que não basta tirar 10 apenas em Física ou apenas em Matemática. Para ganhar o presente, é necessário tirar 10 nas duas disciplinas. Se por outro lado ele dissesse: se você tirar 10 em Física ou Matemática, lhe darei um presente; aí bastaria tirar 10 em uma das matérias.
O que os matemáticos fizeram foi dar um aspecto matemático à lógica, além de aprimorá-la. Mas a idéia fundamental é antiga. Agora vamos à prática.
Na lógica vamos estudar sentenças declarativas (ou proposições). Essas proposições devem satisfazer a dois princípios fundamentais:
1. Uma alternativa só pode ser verdadeira ou falsa;
2. Uma alternativa não pode ser verdadeira e falsa; é lógico
Assim sendo, uma proposição pode ter valor lógico falso (F ou 0) ou verdadeiro (V ou 1)
As proposições são indicadas pelas letras latinas minúsculas: p, q, r, s, t,
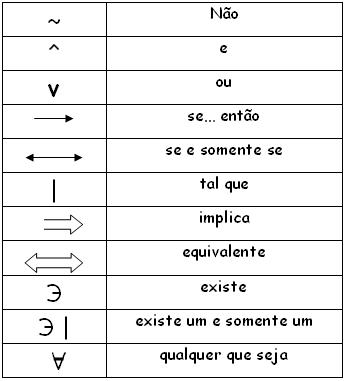
Vejamos agora alguns símbolos usados na Lógica Matemática:
Vejamos alguns exemplos de proposições com valores lógicos definidos.
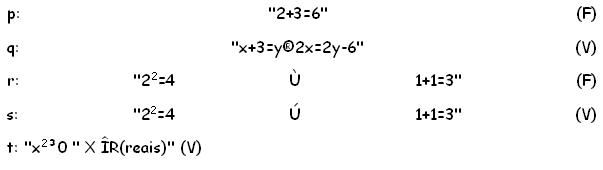
Operadores Lógicos
Através dos operadores lógicos Ù(conjunção) , Ú(disjunção) , ®(condicional) e «(bi-condicional), podemos combinar as proposições lógicas, formando as proposições compostas pÙq, pÚq, p®q, p«q. Observe que nos
exemplos acima houve várias proposições compostas.
Se eu souber o valor lógico de cada uma das proposições p e q, tenho como saber todas as proposições compostas a respeito de p e q. Estas relações estão expressas na tabela abaixo. Chama-se Tabela Verdade. Aí vai a tabela:
Note que podem surgir algumas proposições estranhas a partir da tabela verdade, usando-se os operadores ® e «.
Ex.: “2 é menor que 3 se e somente se x < x+1.” (V)
“Se 2=3 então a Terra é um planeta.” (V)
O que acontece é que esses operadores foram pensados de forma que a primeira proposição fornecesse base para o raciocínio da segunda. Porém, podemos estabelecer p e q como duas proposições sem nenhuma relação.
Tautologia
É uma proposição cujo valor lógico é sempre verdadeiro.
Contradição
É uma proposição cujo valor lógico é sempre falso.