Estudo de um satélite em órbita
As Leis de Kepler diz que qualquer satélite de qualquer planeta, pode estar em órbita circular ou elíptica, mantendo seu movimento através da força de atração gravitacional, que é aplicada pela Terra.
Em relação à órbita elíptica, devemos considerar sua velocidade como sendo linear de translação, onde ela é variável, e apresentando um movimento não uniforme.
Velocidade linear de translação:
Considerando a massa de um planeta representado por M, o raio da órbita representado por r e a constante gravitacional representada por G, temos que a essa força gravitacional aplicada no satélite pelo planeta, irá realizar o papel de uma resultante centrípeta, vejamos:
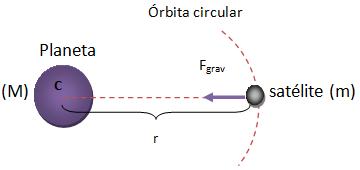
Com base na figura acima, podemos tirar que:

Como falamos anteriormente, G representa a constante universal, portanto podemos concluir que a velocidade de translação possui um módulo que depende tanto da massa do planeta como do raio de sua órbita.
Ao se tratar do mesmo planeta, é importante saber que quanto mais próximo o satélite estiver, mais alta será a velocidade de translação.
Quando se trata do Sistema Solar, devemos considerar Mercúrio, como o planeta que possui a maior velocidade escalar média de translação, já Plutão, o que possui a menor velocidade escalar média de translação.
Período de translação (T)

Contudo podemos concluir que todo o período de um satélite irá depender tanto da massa do planeta, como do raio de sua órbita.
Energia
Vejamos os três tipos de energia:
1- Energia cinética:

2- Energia potencial
Para podermos descobrir a energia potencial gravitacional, devemos usar a seguinte expressão:
Se pensarmos em comparar a expressão da energia cinética, com a expressão da energia potencial, teremos:
3- Energia mecânica
Como vimos nos conteúdos anteriores, a energia mecânica é considerada a soma de duas energias, ou seja, ela é a soma da energia cinética com a energia potencial, portanto temos:
Em = Ecin + Epot = Ecin + (-2 Ecin)
Portanto:
Imponderabilidade no interior do satélite
Primeiramente vamos explicar o que significa imponderabilidade.
A imponderabilidade pode ser considerada como uma ausência de peso, e no caso dos satélites essa imponderabilidade é considerada uma sensação dessa ausência, ou seja, dentro de uma nave em órbita, os corpos são capazes de flutuarem. Isso não quer dizer que não exista força gravitacional, é que é somente usada a resultante centrípeta dessa força, para fazer com que o corpo se mantenha em órbita.
Neste caso não existe troca de forças de compressão com o astronauta e o chão da nave. Podemos citar um exemplo da Terra, quando uma pessoa está dentro de um elevador em queda livre, a pessoa consequentemente não irá se submeter a uma compressão no chão do elevador.
É comum dizermos que um corpo quando está em órbita, não possui peso. Quando falamos isso, estamos afirmando que qualquer objeto que estiver dentro de um satélite e também o satélite apresenta uma queda livre com a mesma aceleração em sua órbita com relação ao planeta. Essa aceleração é imposta através da atração gravitacional do planeta.
Manutenção da órbita
Desprezando a perda de energia por causa do atrito com o ar e desconsiderando a influência dos demais corpos celestes, o satélite será mantido em órbita, por causa da gora gravitacional que é aplicada pelo planeta, sem que haja necessidade de combustível, pois o combustível é usado para colocá-lo na órbita desejada, ou até mesmo para mudar suja órbita.
Satélite estacionário
Esses satélites são denominados estacionários, pois eles ficam parados em relação à superfície da Terra, ou seja, ele parece que fica parado no céu.
É importante lembrar que todas as suas órbitas são circulares, e todas estão no plano equatorial.
Existem algumas condições para que o satélite seja estacionário. Vejamos quais são elas:
1- Plano de órbita:
Como vimos anteriormente a órbita deve estar em um plano equatorial.
2- Trajetória:
Como também já vimos anteriormente, a órbita deve ser circular.
3- Período de translação:
O seu período de translação é o mesmo que o período de rotação do planeta.
Satélite rasante
Esse satélite recebe este nome pelo fato de estar junto à superfície da Terra.
Desconsiderando todos os efeitos do ar, iremos ter:
É importante sabermos que a velocidade deste satélite é correspondente à velocidade de lançamento horizontal de certo corpo, para poder transportá-lo no satélite da Terra. Essa velocidade é denominada velocidade cósmica primeira.