As Leis de Kepler (1571-1630)
 |
O astrônomo Tycho Brahe (1546-1601) realizou medições de notável precisão. Johannes Kepler (1571-1630), discípulo de Tycho Brahe, utilizando os dados colhidos por seu mestre, descreveu, de modo singelo e preciso, os movimentos planetários. |
1ª Lei (Lei das órbitas):
– Tomando o Sol como referencial, todos os planetas movem-se em órbitas elípticas, localizando-se o Sol em dos focos da elipse descrita.

O que é uma elipse?
Denomina-se elipse uma curva correspondente ao espaço geométrico de todos os pontos de um plano, onde a distância entre dois pontos fixos do plano é considerada uma soma constante. Esses pontos fixos são denominados focos da elipse.
Vejamos uma elipse:
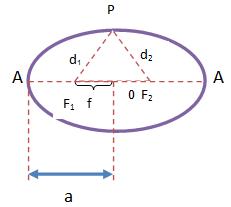
Em relação ao ponto P da elipse acima, temos:
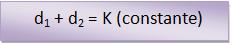
Como podemos observar na elipse acima, existe uma distância entre os pontos A e A, essa distância é considerada uma medida denominada eixo maior da elipse.
Já a letra a é o semi eixo maior, e o f representa a medida da semi distância focal. Podemos adotar e para representar a excentricidade da elipse.
Vejamos:

Se e = 0, a elipse irá se degenerar dentro de uma circunferência, ou seja, no caso da elipse acima, F1 e F2 irão coincidir com 0.
O tamanho da elipse irá depender do valor de e, ou seja, quanto maior for o valor de e maior será a elipse.
Já quando e = 1, irá se degenerar em um único segmento de reta.
Enunciado da 1ª Lei de Kepler
É importante sabermos que todas as órbitas que são expostas por todos os planetas em volta do Sol, estarão localizadas em um dos focos.
Vejamos agora uma tabela que apenas Mercúrio e Plutão apresentam uma elipse maior, ou seja, uma elipse que contenha maior excentricidade, já os outros planetas apresentam as elipses mais perto das circunferências, ou seja, as que possuem uma excentricidade menor.
Vejamos essa tabela:
Porém é importante sabermos que a órbita de um planeta em volta de uma estrela, teoricamente pode ser circular.
2.a Lei (Lei das Áreas):
Essa lei é referente à parte de um planeta que foi “varrida” pelo raio vetor, durante um intervalo de tempo.
– O segmento de reta traçada do centro de massa do Sol ao centro de massa de um planeta do Sistema Solar varre áreas iguais em tempos iguais.
Importante!
Considerando a figura acima, que representa um planeta em quatro posições de sua órbita elíptica em torno do Sol. O ponto mais próximo do Sol chama-se periélio e o mais afastado, afélio.
a) No periélio, a velocidade escalar de um planeta tem módulo máximo, enquanto que, no afélio, tem módulo mínimo.
b) Do periélio para o afélio, um planeta descreve movimento retardado, enquanto que, do afélio para o periélio, movimento acelerado.
Enunciados da 2ª lei de Kepler:
A) Quando falamos dos raios vetores que ligam os planetas com o Sol, devemos saber que esses raios varrem as áreas iguais nos intervalos de tempos iguais.
Com isso temos que:
B) Se tratando da área que foi varrida pelo raio vetor de um dos planetas, podemos dizer que ela é proporcional ao intervalo de tempo que foi gasto.
Com isso temos que:
Onde K é considerada a constante de proporcionalidade, que pode ser chamada de velocidade areolar do planeta.
c) Essa velocidade areolar é considerada constante, pois ela é a razão entre a área varrida e o intervalo de tempo gasto.
É importante lembrar que essa velocidade é variável, ou seja, ela pode variar de um planeta para o outro, fazendo com que a distância média do planeta ao Sol aumente se tornando mínima para Mercúrio e máxima para Plutão.
Consequência da 2ª lei de Kepler
Como vimos anteriormente à velocidade areolar de um planeta é constante, e por este fator ela pode interferir na velocidade de translação, ou seja, ela não deixa com que a velocidade de translação seja variável.
Como podemos observar na figura acima, A1 e A2, são iguais, porém essa igualdade impede que a medida do arco t1 t2 seja maior do que a medida do arco t3 t 4, portanto podemos concluir que a velocidade de translação em t1 t2 se torna maior do que em t3 t 4, pelo fato do intervalo de tempo ser o mesmo.
Portanto:
Com base na conclusão acima, podemos dizer que o planeta vai chegando próximo do Sol, e a sua órbita elíptica, e com isso sua velocidade de translação vai aumentando. Com isso podemos ver que conforme o Sol vai chegando perto o raio vetor vai diminuindo e para que ele consiga “varrer” a mesma área, o planeta deverá se movimentar mais rápido.
No ponto mais próximo do Sol, a velocidade de translação irá ser a maior. Isso recebe o nome de periélio. Já quando o ponto estiver bem longe do Sol, a velocidade de translação irá ser a menor. Isso recebe o nome de afélio.
Vejamos a ilustração:
Com base na figura acima, podemos observar que o movimento de translação se torna uniforme, pois a órbita do planeta é circular, onde do afélio para o periélio o movimento é considerado acelerado e do periélio para o afélio, o movimento é considerado retardado.
Velocidade média de translação
Com relação a um planeta, essa velocidade possui uma função decrescente em relação à distância média de cada planeta ao Sol.
O planeta mais rápido possui uma velocidade média de 50 Km/s, que é o Mercúrio, sendo que a Terra possui uma velocidade de mais ou menos
30 Km/s.
Considerando as órbitas como circulares, podemos afirmar que a velocidade média possui um valor totalmente inversamente proporcional à raiz quadrada do raio de cada órbita.
Vejamos:
O raio de órbita de Plutão é considerado mais ou menos 100 vezes maior que o raio de órbita de Mercúrio, com isso a velocidade média de Mercúrio chega a ser 10 vezes maior que a de Plutão.
Vejamos:
3.a Lei (Lei dos Períodos):
– Para qualquer planeta do sistema solar, o quociente entre o cubo do raio médio (r) da órbita e o quadrado do período de revolução (T) em torno do Sol é constante.
T é o período de revolução do planeta em torno do Sol (intervalo de tempo também chamado de ano do planeta).
Período de translação ou ano de um planeta
O período de translação de um planeta é o intervalo de tempo, representado por T, em que o planeta consegue dar uma volta completa em volta do Sol.
Enunciado da 3ª Lei de Kepler
É importante sabermos que dentre os planetas do Sistema Solar, a razão entre o cubo do raio médio da órbita e o quadrado do período de translação, são constantes. Portanto:
Quando falamos de dois planetas, representados por A e B, teremos:
Se tratando da constante de proporcionalidade da 3ª lei de Kepler, temos:
Onde G representa a constante de gravitação universal, e M representa a massa do Sol.
Vejamos algumas observações:
1- Considerando m como a massa do planeta, e M >> m podemos desconsiderar m, quando comparado com M, podendo chegar à expressão da 3ª Lei de Kepler. Vejamos:
2- Quanto menor o tempo de translação do planeta, mais próximo do Sol estaremos, pois quanto mais longe do Sol, mais a velocidade média do planeta vai diminuir, assim aumentando a extensão da sua órbita. Isso é o que podemos chamar de período de translação crescente.
A unidade as astronômica, representada por UA, é considerada a distância média da Terra ao Sol, que vale:
Vejamos agora um quadro que apresenta a variação do período com a distância média ao Sol que é medida em UA.
3- Vejamos alguns fatores que são funções de órbita, ou seja, são totalmente dependentes da massa do Sol e do raio médio da órbita:
– velocidade areolar;
– velocidade média de translação.
Porém esses fatores não são dependentes das características do planeta que está gravitando.
Isso nos mostra que se um corpo celeste resolver gravitar em volta do Sol e na órbita da Terra, ele irá adquirir:
– Uma velocidade areolar igual a da Terra;
– Uma velocidade média de translação, que é de aproximadamente 30 km/s;
– Um período de translação de 1 ano.
4- Todas as Leis de Kepler são válidas tanto para os planetas do nosso sistema solar, como para os corpos que gravitam em volta das grandes massas centrais, ou seja, planetas que estejam em volta de estrelas, satélites tanto naturais como artificiais que estejam em volta de um planeta e corpos celestes que estejam em volta da Lua.
5- Quando falamos a respeito dos satélites da Terra, é importantíssimo ressaltar que:
• Suas órbitas podem ser tanto elíptica como circular;
• Em relação à Terra, podemos afirmar que seu ponto mais próximo é denominado perigeu, e seu ponto mais afastado é denominado apogeu.
• Alguns fatores como a velocidade areolar e a velocidade média da translação, dependem somente da massa da Terra e do raio médio da órbita, porém não dependem da massa do satélite.
• Quanto à translação da Lua, podemos considerar sua velocidade média como ordem de 1,0 km/s, já de um satélite estacionário, consideramos sua ordem como 3,0 km/s e de um satélite rasante 8,0 km/s. Lembrando que esses valores é sem considerar os efeitos do ar.