Geometria Analítica – Parte 1
A Geometria Analítica foi concebida por René Descartes. Aliando a Álgebra à Geometria, ela possibilita o estudo das figuras geométricas, associando-as a um sistema de coordenadas. Desse modo, as figuras podem ser representadas de pares ordenados, equações ou inequações. Neste número do Aprovar iremos estudar o ponto e a reta.
1. SISTEMA CARTESIANO ORTOGONAL
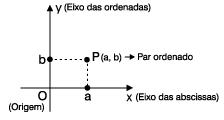
Considere num plano a dois eixos x e y perpendiculares em O. O par de eixos x (Ox), eixo das abscissas, e y (Oy), eixo das ordenadas, chama-se sistema cartesiano ortogonal, onde o plano 
2. ESTUDO DO PONTO
DISTÂNCIA ENTRE DOIS PONTOS NO PLANO CARTESIANO
Quando conhecemos as coordenadas de dois pontos A e B do plano, sabemos localizar esses pontos num sistema cartesiano ortogonal e, assim, podemos calcular a distância entre A e B por meio da seguinte fórmula:
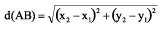
Aplicação
Calcule a distância entre os pontos A (9, 4) e B (1, – 2).
Solução:
Substituindo na expressão:
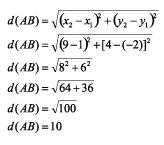
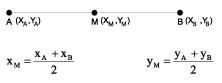
PONTO MÉDIO DE UM SEGMENTO DE RETA
Sejam os pontos A, B, e um ponto M, que divide AB ao meio, podemos dizer que as coordenadas XM e YM do ponto médio M são obtidos por meio da média aritmética das abscissas e ordenadas, respectivamente, dos pontos dos quais M é ponto médio.