É o conjunto dos pontos do plano cuja distância ao ponto C é igual a r.
O ponto C é chamado centro da circunferência e o segmento de reta que liga um ponto qualquer dela ao centro é chamado raio da circunferência. Assim, r é a medida desse segmento.
Resumo:
Equação da Circunferência
1. Equação reduzida

Seja uma circunferência com centro no ponto Q (a, b) e raio r; temos o ponto P (x, y) pertencente à circunferência se, e somente se:
d (Q, P) = r ou 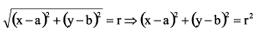
Então, uma circunferência com centro no ponto Q (a, b) e raio r tem equação (x – a)2 + (y – b)2 = r2 (equação reduzida da circunferência).
Observação – Se o centro da circunferência estiver na origem, então a = b = 0, e sua equação será:
x2 + y2 = r2
2. Equação geral ou normal
Desenvolvendo a equação reduzida (x – a)2 + (y – b)2 = r2, vamos obter:
x2 – 2ax + a2 + y2 – 2by + b2 – r2 = 0
Portanto, x2 + y2 – 2ax – 2by + a2 + b2 – r2 = 0 é a equação geral da circunferência.
Observação – A equação normal da circunferência também pode ser apresentada na forma x2 + y2 + Ax – By + C = 0, onde
A = -2a, B = -2b e C = a2 + b2 – r2
Aplicação:
Determine as equações da circunferência de centro (1, 5) e raio 2.
Solução:
Sendo a = 1, b = 5 e r = 2, então, temos:
Sendo a = 2, b = 4 e r = 3, então, temos:
(x – a)2 + (y – b)2 = r2 (x – 1)2 + (y – 5)2 = 22
(x – 1)2 + (y – 5)2 = 4 (equação reduzida)
(x – 1)2 + (y – 5)2 = 4
x2 – 2x + 1 + y2 – 10y + 25 – 4 = 0
x2 + y2 – 2x – 10y + 22 = 0 (equação geral)
Posições relativas entre ponto e circunferência
Quando temos um ponto P (x,y) e uma circunferência C de centro (a,b) e raio r, as possíveis posições relativas de P e C são: