Aplicação
Como a variável x está sob radical de índice par e também no denominador da fração:

Funções Sobrejetora, Injetora e Bijetora
1.º Tipo – Sobrejetora
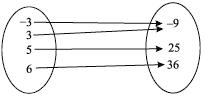
f é sobrejetora Im(f) = CD(f)
A função é sobrejetora se a sua imagem for igual ao seu contradomínio.
2.º tipo – Injetora
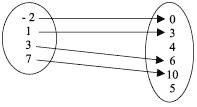
A cada elemento do conjunto A corresponde um elemento distinto do conjunto B. De modo geral, uma função f : A B é injetora se, e somente se, para todo y B existe um único x A, tal que y = f(x).
3.º Tipo – Bijetora
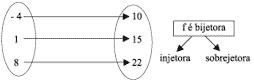
Todos os elementos de B são ../imagens únicas dos elementos de A. De um modo geral a função é bijetora quando é injetora e sobrejetora ao mesmo tempo.
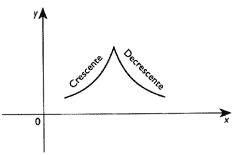
Funções crescente e decrescente
Crescente – À medida que x “ aumenta”, as ../imagens vão “aumentando”
x1 < x2 f(x1) < f (x2)
Decrescente – à medida que x “aumenta”, as ../imagens vão “diminuindo”(decrescendo)
x1 < x2 →F(x1) > f(x2)