Adição e Subtração de Arcos
Considerando a e b como sendo as determinações de dois arcos, temos:
• Cosseno de (a + b)

Demonstração
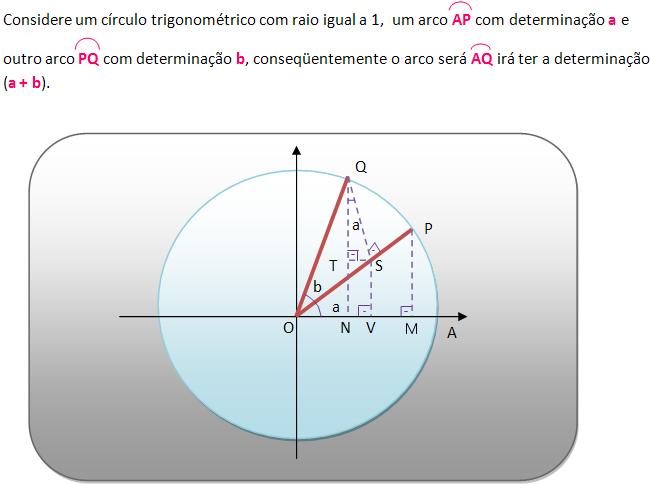
Baseados nas construções geométricas mostradas na representação acima, concluímos que os triângulos OMP, OVS e QTS são retângulos e muito parecidos, ou seja:
I) OM = cos a
PM = sen a
OS = cos b
QS = sen b
ON = cos (a + b)

Como:
ON = OV – NV = OV – TS, resulta em: cos (a + b) = cos a . cos b – sen a . sen b
• Cosseno de (a – b)

Demonstração
Como cos ( – b) = cos b
sen ( – b) = sen b, temos:
cos (a – b) = cos [a + (– b)] =
= cos a . cos (– b) – sen a . sen (– b) =
= cos a . cos b + sen a . sen b
• Seno de (a + b)
• Seno de (a – b)
Demonstração
Como cos (– b) = cos b
sen (– b) = – sen b temos:
sen (a – b) = sen [a + (– b)] =
= sen a . cos (– b) + cos a . sen (– b) =
= sen a . cos b – cos a . sen b
• Tangente de (a + b)
• Tangente de (a – b)