Funções circulares inversas
Introdução
Considerando a função y = f(x), é importante sabermos que é necessário que a função f seja bijetora para definir a função inversa, porém isso não ocorre nas funções trigonométricas, sendo assim necessário limitar os seus domínios.
Essa limitação é feita facultativamente, onde a função f passa a ser considerada bijetora.
Vejamos:
• Função
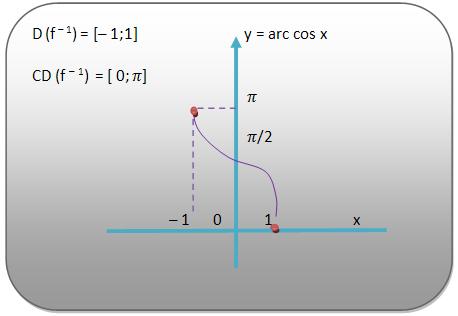
y = arc cos x
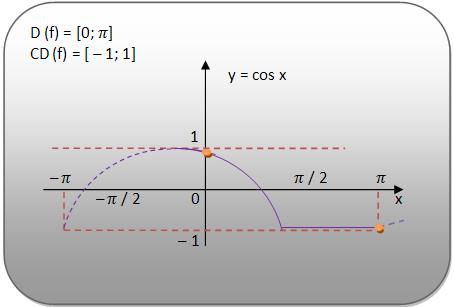
Vejamos uma função y = cos x contendo um domínio limitado ao intervalo [0; π] e contradomínio [ – 1; 1]. Assim, podemos dizer que y = cos x é bijetora, podendo assim definir sua função inversa, que é y = arc cos x.
Vejamos os gráficos:
• Função
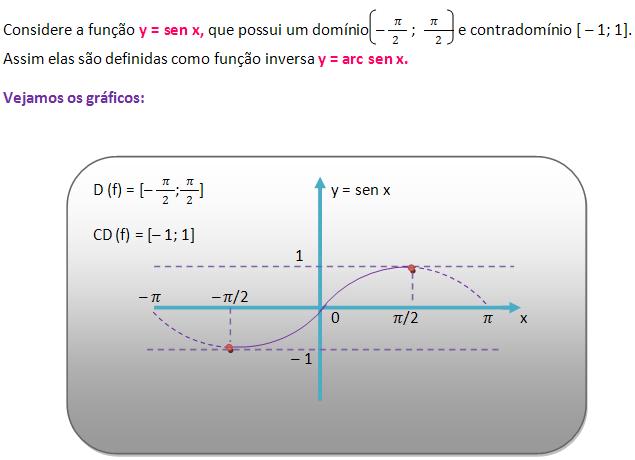
y = arc sen x
• Função
y = arc tg x
De modo análogo, têm-se as funções: y = arc cotg x
y = arc sec x
y = arc cossec x