Potênciação

Função Exponencial

Revisão sobre potenciação
1. Potência com expoente natural

Dado um número real a e um número natural n diferente de zero, chama-se potência de base a e expoente n o número aⁿ que é igual ao produto de n fatores iguais a a.

aⁿ = a . a . a… a, onde:

a = base

n = expoente

Exemplos:
4⁴ = 4 . 4 . 4 . 4 = 256

(-4)³ = (-4) . (-4) . (-4) = -64

Observação: Para n = 1, temos: a¹ = a

Exemplo:

6¹ = 6

Propriedades

Dados a e b reais e m e n naturais, as seguintes propriedades são válidas: 

Observação: para expoentes iguais a zero, convencionou-se que a a⁰ = 1, com a diferente de zero.

2. Potência com expoente inteiro negativo 

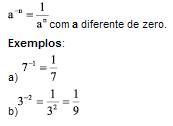
3. Potência com expoente racional fracionário 

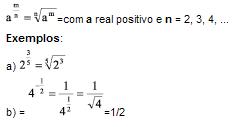
Função exponencial

Dado um número real a (a > 0 e a 1), denomina-se função exponencial de base a uma função f de *+ por f(x) = a^x ou y = a^x.

Exemplos: 

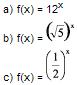
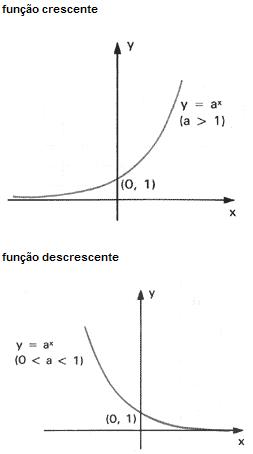
Gráfico da função exponencial

Com relação ao gráfico da função exponencial, temos:

a) D(f) = , CD(f) = *+ e Im(f) = *+

b) O gráfico é uma curva exponencial, que passa por (0, 1).

c) O gráfico não toca o eixo x e não tem pontos nos quadrantes III e IV.

d) Para a > 1 a função é crescente.e) Para 0 < a < 1, função é decrescente: