6. ESTUDO DO SINAL
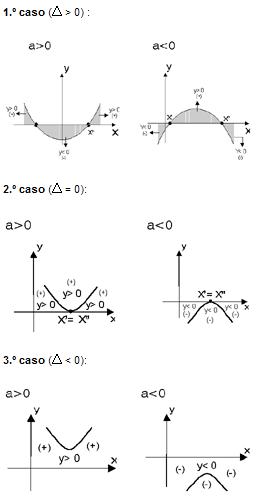
O estudo do sinal da função do 2.º grau é feito determinando-se os seus zeros (caso existam) e analisando o esboço do gráfico.
Aplicação
Lembre-se de que o valor de está relacionado com as raízes e o valor de a determina a concavidade da parábola que a representa.
Exemplo: Estude a variação de sinal da função 3x2 – 4x + 1.
a) Zeros da função: 1/3 e 1.
b) A parábola corta o eixo x nos pontos de abscissas 1/3 e 1. Como a = 3 > 0, sua concavidade está voltada para cima.
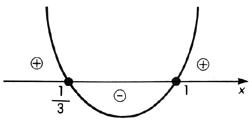
Examinando a figura, temos:
I. y > 0, para x > 1/3 ou x > 1;
II. y = 0, para x = 1/3 ou x = 1;
III. y < 0, para 1/3 < x < 1.
7. INEQUAÇÕES DO 2.º GRAU
A partir do estudo dos sinais da função do 2.º grau, podemos resolver inequações de mesmo grau ou inequações que apresentem produtos ou quocientes de trinômios de 2.º grau. Tais inequações podem também apresentar binômios de 1.º grau, já estudados no tablóide anterior.
Aplicação
Resolver a inequação
(-x2 + 3x +4).(x – 2) < 0
Essa é uma inequação produto em que um dos fatores é um trinômio de 2.º grau e o outro é um binômio de 1.º grau.