Definição

Inequação do 1° grau é toda a sentença aberta do tipo:
ax + b > 0
ax + b ≥ 0
ax + b < 0
ax + b ≤ 0

Onde a ∈ R* e b ∈ R.

Como resolver

Uma inequação do 1° grau em R, do tipo ax + b > 0, basta determinar o conjunto de todos os valores da variável x para os quais o gráfico de f(x) = ax + b está acima do eixo x.

Uma inequação do 1° grau em R, do tipo ax + b < 0, basta determinar o conjunto de todos os valores de x para os quais o gráfico de f (x) = ax + b está abaixo do eixo x.
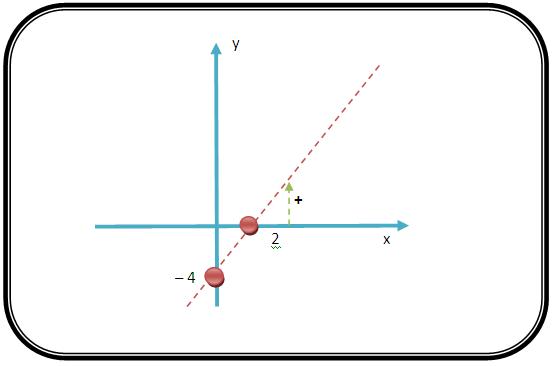
O conjunto solução da inequação 2x – 4 > 0, é {x ∈ R I x > 2}, pois o gráfico de f (x) = 2x – 4 é

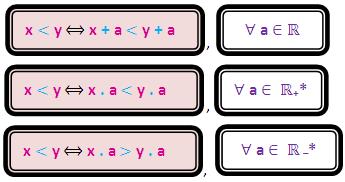
A maneira mais prática é “isolar x”, mas lembre-se que:

O conjunto verdade da inequação 2x + 8 < 0 é {x ∈R I x < – 4}.
2x + 8 < 0 → 2x < – 8 ⟺ x < – 4

O conjunto verdade da inequação – 4x + 12 > 0 é {x ∈ R I x < 3}.
– 4x + 12 > 0 → – 4x > – 12 → 4x < 12 → x < 3