1. DEFINIÇÃO 

Chama-se função do 1.° grau toda função definida de  por f(x) = ax + b com a, b e a 0.

Exemplos:

f(x) = 5x – 3, onde a = 5 e b = – 3 (função afim)

f(x) = 6x, onde a = 6 e b = 0 (função linear)

f(x) = x, onde a = 1 e b = 0 (função identidade)

2. GRÁFICO DA FUNÇÃO DO 1.º GRAU

O gráfico de uma função do 1.º grau é uma reta não-paralela nem ao eixo x nem ao eixo y. Seu domínio é D(f) = e sua imagem é Im(f) = .

1.º exemplo: Construir o gráfico da função y = 3x + 1 (a = 3 > 0)

Resolução: Sabendo que o gráfico da função y = 2x + 3 é do 1.º grau, precisamos somente conhecer dois de seus pontos para traçá-lo. Esses dois pontos podem ser obtidos atribuindo-se dois valores arbitrários para x e determinando suas ../imagens (y).

Para x = 0 y = 3

Para x = – 2 y = -1

Para x = – 1 y = 1


Conclusão:

Se a > 0, a função y = ax + b é crescente.

Se a < 0, a função y = ax + b é decrescente.

3. ZERO OU RAIZ DA FUNÇÃO DO 1.º GRAU

Chama-se zero ou raiz da função do 1.º grau f(x) = ax + b o valor de x para o qual f(x) = 0.

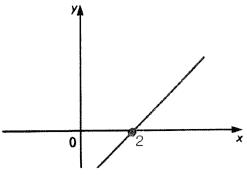
Exemplo: Calcular o zero da função y = x – 2.

x – 2 = 0 x = 2

Observação: geometricamente, o zero da função do 1.º grau é a abscissa do ponto em que a reta corta o eixo x. Então, no exemplo, temos: