3 – Agrupamentos
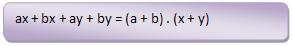
No entanto, se agruparmos ax + bx ou ay + by podemos colocar em evidência tanto o x quanto o y. Assim, a expressão transforma-se em duas parcelas, e em ambas aparecerá um novo fator comum a + b, também podendo ser colocado em evidencia.
Observe
ax + bx + ay + by = x . (a + b) + y . (a + b) = (a + b) . (x + y)
Exemplos
ax + ay + 2x + 2y = a (x +y) +2 . (x + y) = (x + y) . (a + 2)
mm + 3m + 4n + 12 = m . (n + 3) + 4 . (n + 3) = (n + 3) . (m + 4)
a2 – ab – 2a + 2b = a . (a – b) – 2 . (a – b) = (a – b) . (a – 2)
a2 + ab + a + b = a . (a + b) + 1 . (a + b) = (a + b) . (a + 1)
mn – m – n + 1 = m . (n – 1) – 1 . (n – 1) = (n – 1) . (m – 1)