6. Limites tendendo ao infinito

O limite de uma função polinomial, quando x é calculado a partir do termo de maior grau, ou seja, 

A imagem da função tende a um número muito grande quando x aumenta cada vez mais.

7. Função Racional 
Chama- se função racional a toda função da forma , onde P(x) e Q(x) são polinômios.

O limite x, tendente a , de uma função racional é calculado tomando- se o termo de maior grau no numerador e no denominador, ou seja,


Aplicação

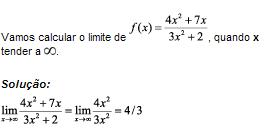
Observações:

a) Se o grau do numerador for menor que o grau do denominador, então o limite será igual a zero.

b) Se o grau do numerador for igual ao grau do denominador, basta dividir os coeficientes dos termos de maior grau.

8. Limites Irracionais

São limites que envolvem funções que se apresentam sob um radical. O problema maior será “levantar” possíveis indeterminações que surgem no cálculo desses limites. No entanto a grande maioria desses problemas é resolvida racionalizando- se a expressão que envolve radical, ou seja,


9. Limite Trigonométrico