Máximos ou Mínimos Relativos

A partir do sinal da derivada de Segunda ordem de uma função f, além da concavidade, podem-se obter pontos de máximo ou mínimos, relativos a um certo intervalo desta função. Sendo o gráfico a seguir de uma função qualquer, tem-se:

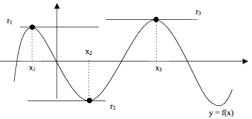
x1= abscissa de um ponto de máximo local.

x2= abscissa de um ponto de mínimo local.

x3= abscissa de um ponto de máximo local.

As retas tangentes r1, r2 e r3 nos pontos de abscissas x1, x2 e x3, respectivamente, são paralelas ao eixo x, logo, a derivada de f anula-se para x1, x2 e x3, ou seja, f’(x1) = f’(x2) = f’(x3) = 0.

Observação:

Nos pontos de mínimo ou máximo relativo, a derivada primeira anula–se.

Teste da derivada de 2.ª ordem

A fim de verificar se um ponto, que anula a derivada primeira de uma função, representa um ponto de máximo ou mínimo local, faz-se o teste da derivada de segunda ordem, ou seja:

a) deriva-se a função;

b) iguala-se a derivada primeira a zero;

c) Seja a função duas vezes diferenciável no intervalo aberto I.
(i) se f(x) (segunda derivada) >0 para todo x em I(intervalo), então o gráfico de f possui concavidade para cima em I
(ii) se f(x) <0 para todo x em I, então o gráfico de f possui concavidade para baixo em I.

Teste da segunda derivada para extremos relativos

Seja a função f diferenciável no intervalo aberto I e suponha que c seja um ponto em I, tal que f (x) (primeira derivada) = 0 e f (x) (segunda derivada) exista.

(i) se f (c) >0, então f possui um mínimo relativo em c.
(ii) se f (c) < 0, então f possui um máximo relativo em c.

Pode ser escrito de outra forma:

Teste da Derivada segunda

Suponha que f (2 derivada) seja contínua na proximidade de c.
(i) se f (c) =0 e f (c) >0, então f tem um mínimo local em c.

(ii) se f (c) = 0 e f (c) <0, então f tem um máximo local em c. 

Regra de L’Hospital
Ao resolvermos exercícios relacionados com limites, é muito frequente o aparecimento de indeterminações do tipo:

Tais indeterminações podem ser levantadas pela Regra de L’Hospital, ou seja, deriva-se separadamente o numerador e o denominador da função dada, tantas vezes quantas necessárias.

Aplicando a Regra de L’Hospital 

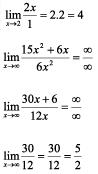
Observação:

A Regra de L’Hospital só pode ser utilizada quando o limite existir e a indeterminação for