Estudo das Derivadas

Interpretação Geométrica

O valor numérico da derivada de uma função

y = f(x) no ponto de coordenadas (x0 ; y0) é o coeficiente angular da reta tangente à curva obtida pela função dada neste ponto, ou seja,

y – y0 = m . (x – x0) ou y – y0 = f’(x0) . (x – x0)

Verificação: 

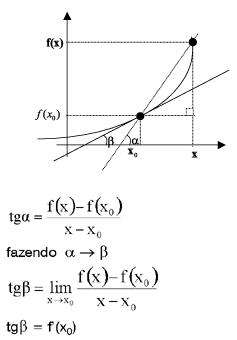
Portanto a equação da reta tangente no ponto de abscissa x0 é:

y – y0 = m . (x – x0) ou

y – y0 = tg . (x – x0) ou

y – y0 = f’(x0) . (x – x0)

Derivada de uma Função

Uma função f diz-se derivável em um certo intervalo aberto, se for derivável em todos os pontos desse intervalo. A função derivada de f, representada por f’, é obtida pelo limite.



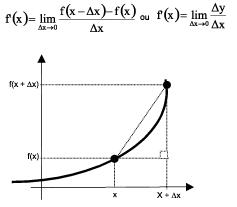
Aplicação

Encontrar a equação da reta tangente à curva

y = x2 – 2x + 1, no ponto de abscissa igual a –2.

Solução:

f(-2) = (–2).(–2) – 2(–2) +1 = 4 + 4 + 1 = 9

y’= 2x – 2

f’(–2) = (–2) – 2 = –4

y – f(–2) = f’(–2).(x + 2) y – 9 = –4(x + 2) r: y = –4x + 1

Regras de Derivação

Por meio da definição, dada anteriormente, da derivada de uma função, provam-se as seguintes regras de derivação.

1. Derivada de uma constante

Sendo K um número real qualquer, tem-se:

f(x) = K→ f’(x) = 0

2. Derivada da função identidade

A derivada da função identidade é igual à unidade.

f(x) = x →f’(x) = 1