3. Derivada de uma função do 1.º grau
A derivada de uma função do 1.° grau é igual ao coeficiente de x.
f(x) = ax + b →f’(x) = a
4. Derivada da função potência
A derivada de uma função potência de x, de expoente genérico “n", é verificada pela definição de derivadas e pelo binômio de Newton.
f(x) = xn→ f’(x) = n . xn-1
5. Derivada do produto de função por uma constante
A derivada do produto de uma constante por uma função é igual ao produto da constante pela derivada da função.
g(x) = K . f(x) →g(x) = K . f (x)
6. Derivada da soma de funções
A derivada de uma soma de unções é igual à soma das derivadas dessas funções.
f(x) = u(x) + v(x)→ f(x) = u(x) + v(x)
7. Derivada da função potência
Sendo u uma função real de x, e sendo n um número real, então a derivada da função y = un é dada por y = un→ y’ = n . un-1 . u’ onde u’ é a derivada de u em relação a x.
8. Derivada do produto de funções
Sendo u e v funções de x, a derivada do produto de duas funções é igual à soma dos produtos de uma das funções pela derivada da outra.
y = u . v →y = uv + uv
onde u e v são as derivadas de u e v, respectivamente, em relação a x.
9. Derivada do quociente de funções
Sendo u e v funções reais de x, a derivada do quociente destas funções é dada pela relação:
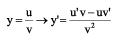
onde u’ e v’ são as derivadas de u e v, respectivamente, em relação a x.
10. Derivada da função exponencial
Sendo “a” um número real ( a > 0 e a 1) e “u” uma função de x, então a derivada da função y = ax é dada por
y = au →y’ = au . lna . u’
Importante:
Como conseqüência desta relação, obtém-se a seguinte fórmula: y = eu →y’ = eu . u’
11. Derivada da função logarítmica
A derivada de uma função logarítmica é dada pela fórmula:

12. Derivada da função seno
A derivada da função seno de um arco u, onde u é a função de x, é:
y = sen u→ y’ = u’ . cos u
13. Derivada da função co-seno
A derivada da função co-seno de um arco u, onde u é uma função de x, é:
y = cos u→ y’ = – u’ . sen u
14. Derivada da função tangente
A derivada da função tangente de um arco u, onde u é uma função de x, é:
y = tg u →y’ = u’ . sec2 u
Importante:
y = sen x →y’ = cos x
y = cos x →y’ = – sen x