Posição dos pontos de um plano em relação a uma reta
Introdução
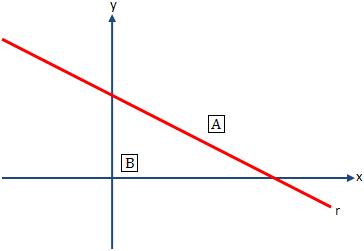
Considere uma reta r de equação ax + by + c = 0, no plano cartesiano:
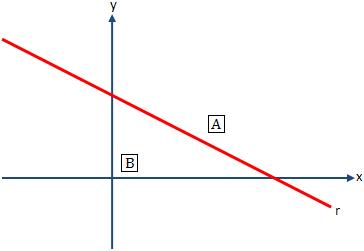
Referindo-se à reta r, os pontos assumem uma das posições relativas a seguir:
– pertencem à reta r.
– pertencem ao semiplano 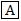
– pertencem ao semiplano 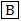
Teorema
Considere P(x0; y0) e (r)a . x + b . y + c = 0 como um ponto e uma reta do plano cartesiano. Podemos verificar que:
• a . x0 + b . y0 + c = 0, para todos os pontos da reta r.
• a . x0 + b . y0 + c > 0, para todos os pontos de um dos semiplanos.
• a . x0 + b . y0 + c < 0, para todos os pontos do outro semiplano.
Posição dos pontos de um plano em relação a uma reta (regras práticas)
Considerando o teorema apresentado, quando tomamos uma reta r, com equação a . x + b . y + c = 0, o ponto P(x; y) do plano cartesiano assume as posições relativas à seguir em relação à reta r:
• pertence à reta r ⇔ a . x + b . y + c = 0
• pertence ao semiplano 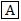
⇔ a . x + b . y + c > 0 (ou a . x + b . y + c < 0) (desconsiderando os pontos de r)
• pertence ao semiplano 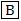
⇔ a . x + b . y + c < 0 (ou a . x + b . y + c > 0) (desconsiderando os pontos de r)