9. Tangentes por um ponto P(x0; y0) externo à circunferência
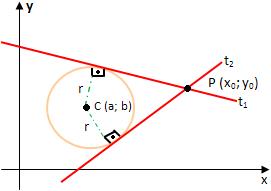
Suponha a circunferência de centro C(a; b) e raio r e o ponto P(x0; y0) externo à circunferência.
A equação do feixe de retas de centro P(x0; y0) é:
y – y0 = m (x – x0) ⇔ mx – y + y0 – mx = 0 (I)
Visto que a reta tangente que procuramos pertence ao feixe de centro P e a distância do centro à reta tangente vale r, resulta:
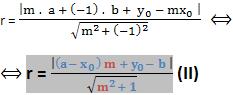
A resolução da equação (II) resulta nos coeficientes angulares (m) das retas que procuramos, que substituídos na equação (I) resultam nas equações das duas tangentes procuradas.