5. Posição dos pontos do plano em relação a uma circunferência 

Considerando uma circunferência (λ), com equação (x – a)2 + (y – b)2 – r2 ou x2 + y2 + m . x + n . y + p = 0, num sistema de coordenadas cartesianas ortogonais, verifica-se que o plano cartesiano permanece dividido em três subconjuntos: 

• Subconjunto dos pontos (x; y) pertencentes a λ.
• Subconjunto dos pontos (x; y) interiores a λ.
• Subconjunto dos pontos (x; y) exteriores a λ.

A posição de um ponto P(x0; y0) em relação à circunferência (λ) é obtida através do cálculo entre a distância do ponto P ao centro C(a; b) da circunferência e em seguida comparando-se com o raio r da circunferência. 

Veja: 

• P pertence à circunferência ⇔ dP,C = r
• P é interno à circunferência ⇔ dP,C < r
• P é externo à circunferência ⇔ dP,C > r 

Obtemos a distância do ponto P(x0; y0) ao centro fazendo a substituição das coordenadas do ponto P na equação da circunferência, isto é:

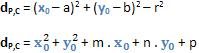
Definição 

Considerando uma circunferência e um ponto P, podemos observar, em geometria plana, que: 

PM . PM’ = PN’ = ……… = PT2 

Esse produto constante é chamado de potência do ponto P em relação à circunferência.